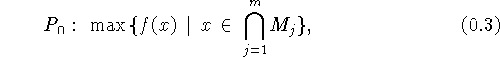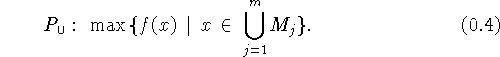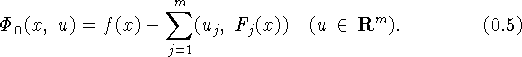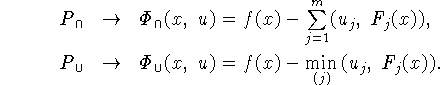

Next: -расширения функциональных
пространств
СИГМА-КУСОЧНЫЕ ФУНКЦИИ
И ЗАДАЧИ ДИЗЪЮНКТИВНОГО ПРОГРАММИРОВАНИЯ
И. И. Еремин
Аннотация:
Рассматривается постановка задачи математического
программирования в ситуации, когда допустимая область задается
объединением множеств, а не их пересечением, - как в традиционной
постановке. Целесообразность рассмотрения такой задачи
подсказывается, например, кусочно-линейным программированием.
Вводится понятие дизъюнктивной функции Лагранжа и
формулируются теоремы типа Куна-Таккера, двойственности, теорема о
точных штрафных функциях и др.
Изучение вопросов кусочно-линейного программирования [1 - 6]
естественным образом приводит к постановке задачи
дизъюнктивного программирования. Произвольная непрерывная
кусочно-линейная функция (k-линейная функция), заданная
на R , допускает стандартное представление в форме
, допускает стандартное представление в форме
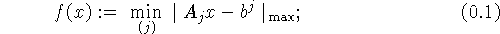
здесь 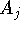 - матрица,
- матрица, 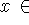 R
R ,
, 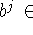 R
R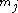 , символ
, символ 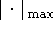 означает взятие максимального значения координат вектора, стоящего
внутри символа
означает взятие максимального значения координат вектора, стоящего
внутри символа 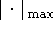 . Произвольная конечная
система неравенств из
. Произвольная конечная
система неравенств из
k-функций конструктивно сводится к
одному неравенству с функцией f(x) вида (1), а произвольная
задача кусочно-линейного программирования (k-линейная
задача) допускает стандартное представление
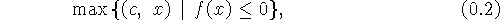
где f(x) имеет вид (1). В отличие от традиционного
представления допустимой области в виде пересечения конечной
совокупности множеств (полупространств, простых выпуклых множеств и
т.д.) в рассматриваемом случае допустимая область задачи
оптимизации (2) задается объединением множеств
(многогранников), т.е.
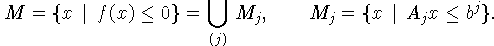
В схеме общей постановки пусть 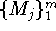 - произвольные
множества из R
- произвольные
множества из R и f(x) - произвольная функция, заданная
на R
и f(x) - произвольная функция, заданная
на R . Запишем задачи
. Запишем задачи
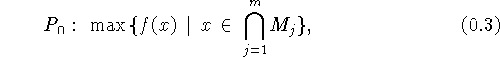
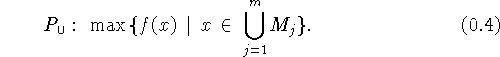
Первую из них назовем задачей в конъюнктивной
постановке, вторую - в дизъюнктивной. Форма (3)
является обычной для задач математического программирования. Вторая
из них отражает ситуацию кусочно-линейной задачи (2). Пусть
в (4):  ,
, 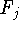 : R
: R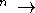 R
R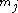 ,
, 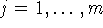 . Для задачи
. Для задачи 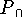 функцией Лагранжа является
функцией Лагранжа является
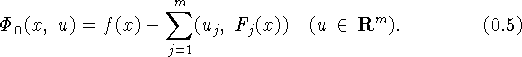
Задаче 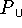 , т.е. (4), поставим в соответствие
функцию
, т.е. (4), поставим в соответствие
функцию
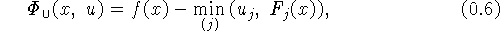
которую будем называть дизъюнктивной функцией Лагранжа
для задачи 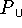 . Зафиксируем схему соответствия задачам
. Зафиксируем схему соответствия задачам
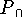 и
и 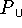 их функций Лагранжа:
их функций Лагранжа:
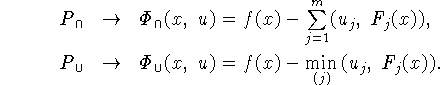
Задаче кусочно-линейного программирования (k-линейной
задаче) в стандартной форме (2) будет соответствовать
дизъюнктивная функция Лагранжа вида
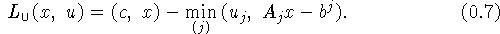
С этой функцией можно связать многие проблемы,
относящиеся к изучению k-задач, часть из которых
рассматривается ниже. Алгебра
k-линейных функций и
k-линейных задач допускает расширение своих постановок до рамок
более общих конструкций, а именно - до рамок
 -
расширений функциональных линейных пространств. Речь идет о
расширении фиксированного линейного функционального
пространства F
-
расширений функциональных линейных пространств. Речь идет о
расширении фиксированного линейного функционального
пространства F до минимального пространства F, замкнутого
относительно операции дискретного максимума, т.е. если
до минимального пространства F, замкнутого
относительно операции дискретного максимума, т.е. если
 F, то
F, то 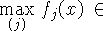 F.
Если F
F.
Если F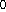 - пространство линейных функций, то F - класс
k-линейных функций; если F
- пространство линейных функций, то F - класс
k-линейных функций; если F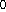 - класс квадратичных функций,
то F - класс кусочно-квадратичных функций, и т.д. Отмеченное
обстоятельство позволяет ряд проблем кусочного
программирования и связанных с ним дизъюнктивных задач оптимизации
выносить за рамки линейных постановок.
- класс квадратичных функций,
то F - класс кусочно-квадратичных функций, и т.д. Отмеченное
обстоятельство позволяет ряд проблем кусочного
программирования и связанных с ним дизъюнктивных задач оптимизации
выносить за рамки линейных постановок.
Хотя кусочно-линейные функции и соответствующий им аппарат имеют
важное значение, тем не менее число работ, посвященных этим
вопросам, незначительно. Отметим работы [1 - 6], первая из
которых, являясь кандидатской диссертацией С.В.Плотникова, содержит
главу III под названием ``Кусочно-линейные функции и полиэдральные
множества'', в которой проводится довольно основательное
исследование по алгебре и геометрии класса k-функций.


Next: -расширения функциональных
пространств