Рассмотрим общую задачу кусочно-линейного программирования в
канонической постановке (4.1), т.е.
с точки зрения ее эквивалентной редукции к задаче этого же типа,
но со снятием основного ограничения в (6.1). Поставим задаче
в соответствие k-задачу
здесь 
- неотрицательный векторный параметр
размерности 
, т.е - число неравенств в системе 
.
Как и в предыдущем параграфе, будем использовать следующие
обозначения: 
- это задача 
, 
, 
- двойственная к ней,
arg, 
, 
.
Теорема 6.1. Пусть задача 
разрешима, 
, 
; 
. Если 
,
, то оптимальные значения и оптимальные множества задач
и 
совпадают, т.е.
Д о к а з а т е л ь с т в о. Обозначим целевую функцию в (6.2) через 
, а вычитаемую из 
часть - через 
.
Докажем вначале равенство (6.3). Для 
Arg(6.1)
получаем 
opt(6.1), следовательно, opt(6.2)
opt(6.1).
Докажем обратное неравенство. По теореме :
С учетом этого неравенства оценим для 
:
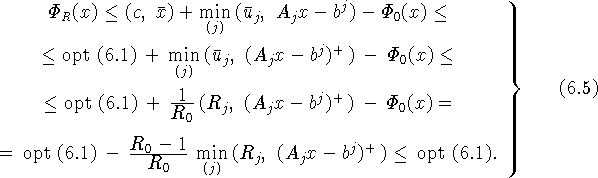
Отсюда 
opt(6.1). Таким образом, равенство (6.3) доказано.
Из него, в частности, следует включение Arg(6.1)
Arg(6.2), что позволяет, на самом деле, в
задаче (6.2) вместо 
писать 
. Докажем
обратное включение. Пусть Arg(6.2).
Согласно (6.5) имеем:
Отсюда вытекает
а потому 
: 
, что ввиду 
дает 
. Следовательно, 
. Допустимость вектора 
для
задачи (6.1) вместе с 
opt(6.1)
означает Arg(6.1), а потому и Arg(6.2)Arg(6.1). Доказательство равенства (6.4) также
завершено.
Конструкция доказательства может быть повторена для более общей
ситуации, а именно для задачи (2.1) и эквивалентной редукции ее к
задаче
Справедлива
Теорема 6.2. Пусть каждая из задач 
, 
, обладает седлом 
. Тогда при 
,
задачи 
и 
эквивалентны в
смысле совпадения их оптимальных значений и оптимальных множеств.
Действительно, в соответствии с теоремой можно
выписать неравенство
а далее все повторить в соответствии с выкладками (6.5).