2. Задача о седловой точке дизъюнктивной функции Лагранжа

Рассмотрим задачи (3) и (4) с их функциями Лагранжа соответственно (5) и (6). Задачу (4), в которой , , можно переписать в виде
 
Здесь ограничения задачи (4) мы дополнили требованием неотрицательности вектора x, т.е. . Это связано с обеспечением симметрии в постановках двойственных задач. Под множествами , следовательно, будут пониматься , . Если - функция (6), то с (2.1) связывается задача о седле :
 
В математическом программировании хорошо известен факт [7] (впрочем, просто доказываемый):

Если - седло функции Лагранжа , поставленной в соответствие задаче , то , и Arg(3).

Для задачи (2.1) и ее дизъюнктивной функции Лагранжа имеет место аналогичное утверждение.

Теорема 2.1.  Если - седловая точка для , то и .

Д о к а з а т е л ь с т в о. В соответствии с (2.2) имеем:
 

 

Соотношение (2.4) перепишем в виде
 
Докажем, во-первых, , т.е. . Если бы
, , то за счет выбора можно было бы значение правой части в (2.5) сделать как угодно большим, что противоречило бы соотношению (2.5). Доказанное дает: . На самом деле, . Если бы , то соотношение (2.5) при u = 0 порождало бы противоречивое неравенство . Итак, соотношение доказано.

Необходимо доказать оптимальность вектора  для (2.1), т.е.
, . Обратимся к соотношению (2.3), которое можно теперь пареписать в виде
 
Если , т.е. при некотором , то , что в силу (2.6) дает , . Теорема доказана.

В математическом программировании (МП) более важной является обратная теорема, формулирующая условия, гарантирующие существование седловой точки для соответствующей функции Лагранжа. Такие теоремы имеют место для разрешимых задач линейного программирования (ЛП), выпуклого программирования (ВП) с условиями регулярности и некоторых других классов задач МП. Для дизъюнктивных постановок задач МП ситуация усложняется. В частности, усиливаются требования типа регулярности.

Задачу (2.1) назовем вполне регулярной, если каждая из задач
 
разрешима. Эквивалентом такой регулярности является разрешимость задачи и непустота всех .

Пусть - функцияЛагранжа для (2.7), здесь , .

Теорема 2.2.  Пусть каждая из функций обладает седлом
, . Если - то значение , на котором достигается , то
 
где .

Д о к а з а т е л ь с т в о. Во-первых, имеем: , и , . Отсюда , но поскольку левая часть этого неравенства равна , то доказываемое неравенство (2.8) верно.

Несколько модифицируем функцию , а именно, положим

где ``+'' над означает положительную срезку. Справедлива

Теорема 2.3. 

1)

Для справедливы теоремы и .

2)

В условиях теоремы  точка (из этой теоремы) реализует седло для .

Д о к а з а т е л ь с т в о. Что касается утверждений из формулировки 1), то они проверяются так же, как и теоремы и . Рассмотрим утверждение 2). Требуется доказать


 
Так как реализует , пусть , то , а потому при любых , . Поэтому, в частности, . В силу сказанного правое неравенство в (2.9) выполняется очевидным образом для любых , а левое повторяет доказанное неравенство (2.8) (на случай функции ). Теорема доказана.

З а м е ч а н и е к формулировкам теорем - . Доказанные теоремы носят довольно общий характер. В них не уточняется, например, постановка задач (2.7). Но если, скажем, (2.7) - задача выпуклого программирования, то вместо постулирования существования седла для их функций Лагранжа (в теореме ) можно было бы предположить разрешимость задач (2.7) и выполнимость условия: , (условие регулярности). Этим бы и гарантировалось существование седла для , . Что касается случая линейной постановки задачи (2.1), то ниже дается уточнение соответствующих теорем. Заметим, что линейный случай имеет самостоятельный интерес в связи с актуальностью задач кусочно-линейного программирования.

Если

- общая постановка задачи кусочно-линейного программирования, т.е. - кусочно-линейные функции, то ее можно эквивалентно переписать в виде

а потому и в виде

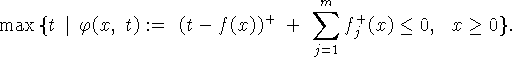
Так как также кусочно-линейная функция от , то эту задачу можно привести к виду (1.10), соответствующему той ситуации, когда F - пространство линейных функций. Этим самым мы подчеркнули, что произвольную задачу кусочно-линейного программирования
(k-линейную задачу) можно записать в форме
 
или

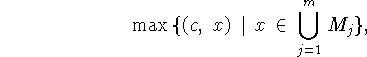
где , .

Итак, далее речь идет о задаче (2.10) и ее функции Лагранжа в форме

Лемма 2.1.  Пусть задача  разрешима и , (т.е. вполне регулярна). Тогда функция обладает седлом , причем в качестве и выступают:



где .

Д о к а з а т е л ь с т в о. Если показать, что , то в силу теоремы  левое неравенство в определении седла для будет выполнено. Так как вектор удовлетворяет одной из систем , то . Покажем . Имеем:



Выше мы воспользовались соотношениями: - по теореме двойственности в ЛП; .

Остается показать выполнимость правого неравенства в определении седловой точки для , т.е.

С учетом выписанное неравенство принимает вид
 
Так как , то при любом , следовательно, (2.11) верно. Лемма доказана.

Отсюда и теоремы  вытекает

Теорема 2.4.  Если системы совместны, то задача  разрешима тогда и только тогда, когда ее дизъюнктивная функция Лагранжа

обладает седлом , при этом

1)

если разрешима и , , , то - седло;

2)

если - седло для , то удовлетворяют всем соотношениям из 1).