Задача разделимости непересекающихся множеств M и
N из некоторого пространства X с помощью функции f(x) из
фиксированного класса 
называется задачей
дискриминацией множеств. Функция f(x) в этом случае называется
дискриминантной. Разделимость состоит в выполнимости
неравенств
Можно говорить и о не строгой разделимости, когда в (7.1)
допускаются не строгие неравенства.
Если M и N - выпуклые многогранники, а
- класс аффинных функций, то говорят о задаче линейной
дискриминации. Задача линейной дискриминации является одной из
важнейших задач в распознавании образов (РО). В качестве одной из
базовых формальных моделей РО является система строгих линейных
однородных неравенств. Убедимся в этом.
Пусть 
и 
- некоторые
образы, 
R
и 
R -
формализованные выборки
представителей этих образов. Если
- некоторый базовый набор функций (вообще говоря, произвольный),
то разделяющую функцию можно искать в ви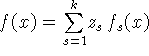де 
, где 
- числовые
коэффициенты. Свойство разделимости состоит в выполнимости системы
неравенств:
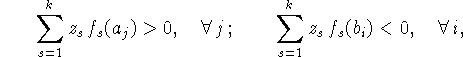
или в матричном виде
где 
, 
;
, 
.
Если 
-
некоторое решение системы (7.2), то функция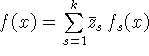 
будет строго разделяющей множества A и
B. Дискриминантная функция f(x) реализует правило соотнесения
(по свойству принадлежности одному из образов и
), предъявляемого для распознавания вектора y по правилу:
Функция f(x) реализует решающее правило.
Система (7.2) может быть как совместной, так и несовместной.
На случай несовместности имеется обобщение понятия решения как
конечной совокупности векторов 
R (именуемой
комитетным решением) такой, что любое из неравенств
системы (7.2) удовлетворяется более чем половиной векторов этой
совокупности. Комитетная технология и ее использование в задачах
распознавания составляют важное и хорошо разработанное направление в
распознавании образов [8].
Если M и N - многогранники, причем 
, то эти множества строго разделяются аффинной функцией.
Ниже речь пойдет о разделимости произвольных непересекающихся
полиэдральных множеств кусочно-линейной функцией (k-функцией).
Итак, пусть 
, 
, 
и 
-
конечные совокупности выпуклых многогранников, причем . Имеет место
Теорема 7.1. Полиэдральные множества M и N с пустым пересечением
строго разделяются k-функцией, т.е. функцией вида 
Д о к а з а т е л ь с т в о. Полиэдральное множество может быть задано одним
k-неравенством: если 
и
, то
где f(x) - функция (7.3);
где 
.
Учитывая соотношения: X
,
X
, при любых 
и
будем иметь
Таким образом, построена функция 
, зависящая от числовых параметров и , строго разделяющая полиэдральные множества M
и N.
Следствие 7.1. Пусть 
и 
- конечные совокупности точек
из , при этом 
. Тогда существует k-функция f(x), строго
разделяющая эти множества, т.е.
Д е й с т в и т е л ь н о,
поскольку точка из R может быть задана конечной системой
линейных неравенств (если 
, то
), то сформулированное следствие
превращается в частный случай теоремы .
На самом деле, в данном следствии пространство, из
которого берутся точки, может быть произвольным. Сведение
к конечномерному арифметическому
пространству тривиально: достаточно взять
подпространство E
исходного пространства, натянутое на
совокупность
, выделить его некоторый базис, в котором векторы 
и
б-- т представлены точками конечномерного
арифметического пространства. Если взять прямое
разложение X=E+H, то k-функция f(x),
разделяющая указанные совокупности точек в E, может быть
продолжена до k-функции 
, определенной на всем
пространстве X, по правилу: если 
X и 
, 
E, 
H,
то 
.
Поступила 25.10.97
СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ