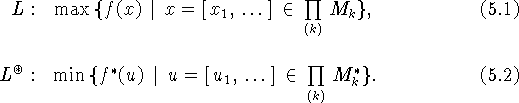
Запишем обобщения задач (4.1) и (4.6) в форме
(4.16) и (4.17), несколько изменив обозначения нумерующих
индексов, а именно: пусть
Задачи (4.16) и (4.17) можно переписать в симметричном
виде
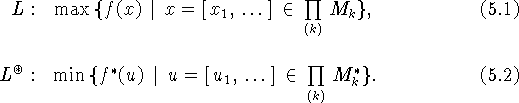
Рассмотрим ситуацию несобственности (неразрешимости) задач L
и 
с позиций построения двойственности. Поскольку
формально эти задачи распадаются на совокупности задач 
и
, то к парам взаимно двойственных задач 
, независимо от их разрешимости или неразрешимости, можно
применить схему двойственности для несобственных задач ЛП (см.,
например, [9, § 6]):
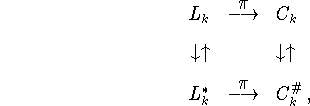
в силу которой задачи 
и 
разрешимы,
при этом opt
opt. Задачи и
в полном соответствии с [9, § 6] имеют вид:
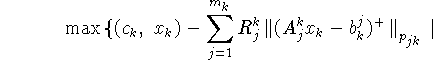
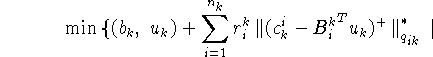
Здесь 
и
- произвольные разрезы матрицы 
на горизонтальные и вертикальные подматрицы,
и 
- соответствующие
этому разрезы векторов 
и 
;
и 
- наборы норм в соответствующих
пространствах; 
и 
- неотрицательные
параметры. Подсистемы 
, 
и
, 
в (5.3) и
(5.4) предполагаются совместными, что при подходяще выбранных
параметрах 
и 
системы ограничений в задачах
и становятся совместными. Смысл теоремы двойственности
для и состоит в равенстве
optopt [9, теорема 6.2].
В основу двойственности для L и может быть
положена схема:
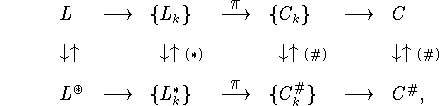
при этом формирование задач C и 
в данной
схеме производится по логике формирования задач (5.1) и
(5.2) из задач и .
Пусть 
и 
- целевые функции в
задачах (5.3) и (5.4), 
и 
-
допустимые множества этих задач; 
, 
.
Сформируем задачи:
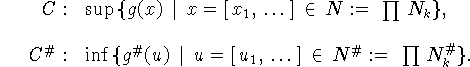
Теорема 5.1. Пусть выполнены условия:
1. Параметры и выбраны так, что системы
ограничений в 
и 
совместны при строгих
неравенствах 
и 
.
2. Все нормы, участвующие в формировании задач 
и
- монотонны.
3. Операция 
в C достижима (ее конечность
следует из условия 1 в силу свойства
,
.
Тогда задача разрешима, при этом 
.
Справедливость этого утверждения следует из основной
теоремы
двойственности для несобственных задач ЛП, на
которую уже была ссылка [9, теорема 6.2], и тех соображений,
которые легли в основу обоснования теоремы .
З а м е ч а н и е 5.1.
Теорема соотнесена к задаче довольно общего вида,
содержит много параметров с широким диапозоном их выбора (разбиения
систем ограничений на подсистемы, выбор норм, назначение числовых
параметров и ). Поэтому она допускает много частных
формулировок, имеющих и самостоятельный интерес. Этот вопрос здесь
детально не рассматривается, так как несколько уводит от основных
акцентов данной статьи.