F
Кусочно-линейные функции - это ![]() -функции в
ситуации, когда
-функции в
ситуации, когда
F![]() - пространство линейных функций.
К определению кусочно-линейных функций можно подойти двояко:
либо так, как это только что сделано в §1, либо исходя из
некоторой аксиоматики, идентифицирующей такие функции. Остановимся
на втором подходе.
- пространство линейных функций.
К определению кусочно-линейных функций можно подойти двояко:
либо так, как это только что сделано в §1, либо исходя из
некоторой аксиоматики, идентифицирующей такие функции. Остановимся
на втором подходе.
Пусть имеются конечные совокупности многогранников ![]() и собственных линейных функций
и собственных линейных функций ![]() . Будем
говорить, что система
. Будем
говорить, что система![]() задает
однозначную кусочно-линейную функцию l(x), заданную
на X, если:
задает
однозначную кусочно-линейную функцию l(x), заданную
на X, если:
Будем использовать обозначения: L![]() -
пространство линейных
-
пространство линейных
функций, L -
пространство k-линейных функций, определенных внешним образом в
силу свойств 1) и 2). На самом деле класс функций L
совпадает с классом F из пре-- ущего параграфа, который строится
из F![]() L
L![]() , т.е. L - это минимальное
расширение пространства линейных функций, замкнутое относительно
операций дискретного максимума (см. §1). Следовательно,
представление (1.9), а также каждое из (1.10) и
(1.11), являются универсальным представлением
кусочно-линейных функций (k-линейных функций).
, т.е. L - это минимальное
расширение пространства линейных функций, замкнутое относительно
операций дискретного максимума (см. §1). Следовательно,
представление (1.9), а также каждое из (1.10) и
(1.11), являются универсальным представлением
кусочно-линейных функций (k-линейных функций).
Для унификации и упрощения записи k-линейных функций, систем
неравенств из k-функций, задач кусочно-линейного программирования и
т.д. будем в дальнейшем полагать: X=R![]() , тогда
, тогда
![]()
![]()
Если ![]() - вектор линейных
функций, то
- вектор линейных
функций, то
![]()
Представления кусочно-линейных функций в виде (1.9) -
(1.11) принимают унифицированную форму:
![]()
![]()
![]()
Отметим также свойства функций дискретного максимума:
![]()
![]()
Произвольная конечная система кусочно-линейных неравенств может
быть записана в виде
![]()
Эта система может быть записана с помощью одного неравенства
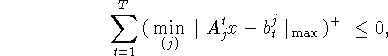
или (на основе теоремы ) в виде
![]()
Это задание будем считать одним из стандартных. Другим
стандартным видом является
![]()
Рассмотрим представление системы в виде (3.5).
Положим ![]() . Тогда
множеством решений неравенства (3.5) будет
. Тогда
множеством решений неравенства (3.5) будет 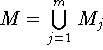 . С другой стороны, если M -
произвольное полиэдральное множество, пусть из R
. С другой стороны, если M -
произвольное полиэдральное множество, пусть из R![]() , т.е.
, т.е. 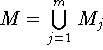 и
и ![]() - многогранники,
т.е.
- многогранники,
т.е. ![]() задаются конечными системами линейных неравенств:
задаются конечными системами линейных неравенств: ![]() , то M является множеством решений
неравенства (3.5).
, то M является множеством решений
неравенства (3.5).
С этой же точки зрения посмотрим на неравенство (3.6).
Пусть
![]()
![]()
(L![]() - пространство аффинных функций). Положим
- пространство аффинных функций). Положим
![]()
Тогда, как легко видеть, ![]() совпадает с множеством решений неравенства (3.6). Тем самым, для
неравенства (3.6) указаны те многогранники
совпадает с множеством решений неравенства (3.6). Тем самым, для
неравенства (3.6) указаны те многогранники ![]() , объединение
которых и дает множество решений неравенства (3.6). С другой
стороны, если полиэдральное множество M задано тем или иным
образом, например, как в пре-- ущем случае - совокупностью систем
линейных неравенств, каждая из которых задает выпуклую многогранную
компоненту множества M, то требуется цепочка тех или иных
преобразований типа (1.3) - (1.8), приводящая к заданию
множества M одним неравенством вида (3.6).
, объединение
которых и дает множество решений неравенства (3.6). С другой
стороны, если полиэдральное множество M задано тем или иным
образом, например, как в пре-- ущем случае - совокупностью систем
линейных неравенств, каждая из которых задает выпуклую многогранную
компоненту множества M, то требуется цепочка тех или иных
преобразований типа (1.3) - (1.8), приводящая к заданию
множества M одним неравенством вида (3.6).
Наконец, рассмотрим систему кусочно-линейных неравенств в
форме (3.4), формально более сложную, чем (3.5) или
(3.6). Положим
![]()
Множество ![]() - это множество решений t-го неравенства в
системе (3.4), так что M - множество решений всей системы.
- это множество решений t-го неравенства в
системе (3.4), так что M - множество решений всей системы.
Материал, изложенный в §1 и §3, устанавливает способы конструктивного соответствия между полиэдральными множествами и их аналитическим заданием. Хотя сопутствующая этому алгебра преобразований может быть достаточно громоздкой, тем не менее логика этих преобразований проста и может быть в реальных прикладных ситуациях поручена компьютеру.