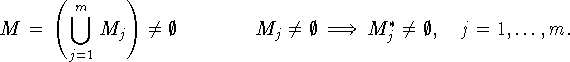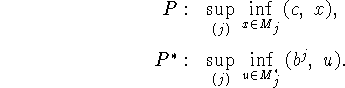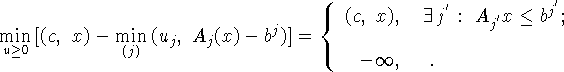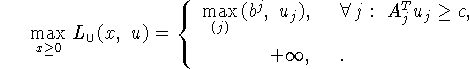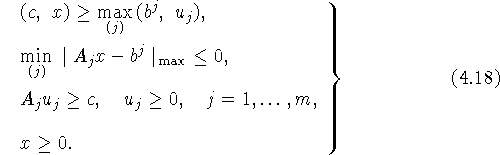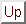

Next: Двойственность для несобственных
Up: СИГМА-КУСОЧНЫЕ ФУНКЦИИ И ЗАДАЧИ
Previous: Кусочно-линейные функции
и
4.1. Предварительные замечания
Произвольной задаче кусочно-линейного программирования, т.е.
задаче поиска экстремума k-линейной функции при ограничениях в
форме конечной системы неравенств с k-линейными функциями в левых
частях, можно, как уже отмечалось, придать универсальный и простой
вид
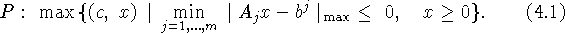
Если же f(x) - произвольная оптимизируемая, пусть
максимизируемая, k-функция при одном k-неравенстве, пусть  (возможно, с
(возможно, с 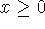 ), то переписав задачу
), то переписав задачу 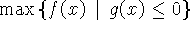 в виде
в виде
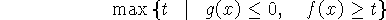
и преобразовав систему из двух k-неравенств к одному
k-неравенству, получим задачу поиска максимума линейной функции при
одном ограничении в форме k-неравенства. В (4.1) ограничение
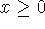 выделено для целей обеспечения симметрии в ряде
аналитических конструкций, рассматриваемых ниже.
выделено для целей обеспечения симметрии в ряде
аналитических конструкций, рассматриваемых ниже.
Итак, объектом рассмотрения примем задачу (4.1). Введем
частичную задачу (подзадачу)
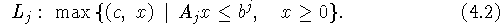
Связь между задачей (4.1) и 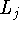 проста:
проста:
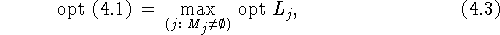
где 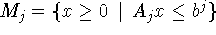 . В (4.2) для
некоторых j множества
. В (4.2) для
некоторых j множества 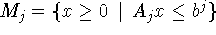 могут быть пустыми при свойстве разрешимости исходной
задачи (4.1), т.е. произвольная k-задача, будучи преобразована
к виду (4.1), распадается на конечное число задач линейного
программирования, решив которые, мы тем самым находим
решение и исходной задачи. Поскольку конструктивизм
соответствующих преобразований обеспечен, то
формально решение произвольной задачи кусочно-линейного
программирования сводится к использованию отмеченного конструктивизма
и некоторого метода (например, симплекс-метода) решения задачи ЛП.
могут быть пустыми при свойстве разрешимости исходной
задачи (4.1), т.е. произвольная k-задача, будучи преобразована
к виду (4.1), распадается на конечное число задач линейного
программирования, решив которые, мы тем самым находим
решение и исходной задачи. Поскольку конструктивизм
соответствующих преобразований обеспечен, то
формально решение произвольной задачи кусочно-линейного
программирования сводится к использованию отмеченного конструктивизма
и некоторого метода (например, симплекс-метода) решения задачи ЛП.
4.2. Условия разрешимости k-задачи
Для k-задач выполняется ряд свойств и теорем, формулируемых в
рамках теории линейного программирования. Некоторые из них являются
следствиями теорем из ЛП, некоторые же требуют своих доказательств,
по крайней мере, уточнений. Не требует самостоятельного доказательства
Теорема 4.1[о достижимости]. Если
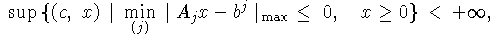
то операция 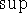 в этой задаче достижима.
в этой задаче достижима.
Выпишем задачу, двойственную к 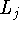 :
:
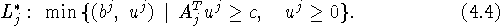
Пусть 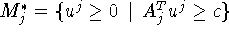 .
.
Теорема 4.2. Задача 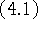 разрешима тогда и только тогда, когда
разрешима тогда и только тогда, когда
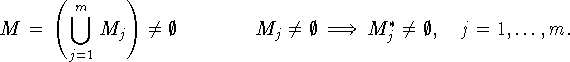
Д о к а з а т е л ь с т в о. Поскольку условия 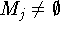 и
и 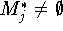 являются необходимыми и достаточными для разрешимости задачи
являются необходимыми и достаточными для разрешимости задачи 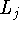 ,
то
,
то 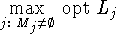 конечен и является значением optP. Обратно, если задача P
разрешима, то все задачи
конечен и является значением optP. Обратно, если задача P
разрешима, то все задачи 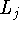 c
c 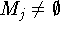 - разрешимы
(т.е. ситуации opt
- разрешимы
(т.е. ситуации opt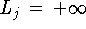 исключаются), а тогда
в соответствии с теоремой двойственности в ЛП:
исключаются), а тогда
в соответствии с теоремой двойственности в ЛП: 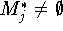 ,
что и требовалось.
,
что и требовалось.
З а м е ч а н и е 4.1.
Другой вариант формулировки теоремы состоит в
эквивалентности
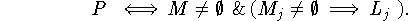
4.3. Двойственность
Исходную k-задачу возьмем в форме (4.1), дополнив ее
предположением (впрочем, несущественным): размерность векторов 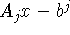 одинакова, т.е. число неравенств в каждой из систем
одинакова, т.е. число неравенств в каждой из систем 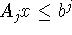 одно и то же. Введенное условие позволяет двойственную
переменную для
одно и то же. Введенное условие позволяет двойственную
переменную для 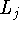 , т.е. переменную
, т.е. переменную 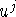 в задаче (4.4),
обозначать одним символом u. В соответствии со сказанным
задачу (4.4) перепишем в виде:
в задаче (4.4),
обозначать одним символом u. В соответствии со сказанным
задачу (4.4) перепишем в виде:
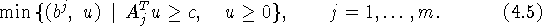
Сформулируем задачу
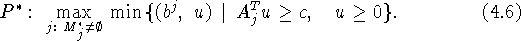
Задачу 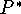 будем рассматривать как один из вариантов задачи,
двойственной к P.
будем рассматривать как один из вариантов задачи,
двойственной к P.
В отношении задачи (4.6) справедлива
Теорема 4.3. Задача 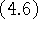 разрешима тогда и только тогда, когда
разрешима тогда и только тогда, когда
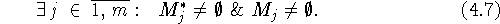
Д о к а з а т е л ь с т в о. Действительно, если 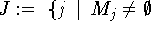 ,
,
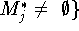 , то для
, то для 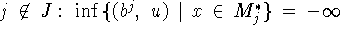 , поэтому в (4.6) максимум
можно брать только по
, поэтому в (4.6) максимум
можно брать только по 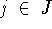 . Этим и обеспечивается разрешимость
задачи
. Этим и обеспечивается разрешимость
задачи 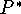 . Необходимость условий (4.7) очевидна: если
. Необходимость условий (4.7) очевидна: если 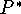 разрешима, то хотя бы для одного j' задача
разрешима, то хотя бы для одного j' задача 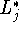 разрешима, что
и эквивалентно (4.7).
разрешима, что
и эквивалентно (4.7).
Из теорем и , а также теоремы
двойственности в ЛП, вытекает
Теорема 4.4. Если задача 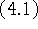 разрешима, то
разрешима, то 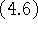 также
разрешима, при этом их оптимальные значения совпадают.
также
разрешима, при этом их оптимальные значения совпадают.
В ситуации задач P и 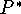 свойство одновременной их
разрешимости или неразрешимости, в отличии от ЛП, теряется.
Принимая во внимание возможность несобственных оптимальных значений,
запишем эти задачи в виде
свойство одновременной их
разрешимости или неразрешимости, в отличии от ЛП, теряется.
Принимая во внимание возможность несобственных оптимальных значений,
запишем эти задачи в виде
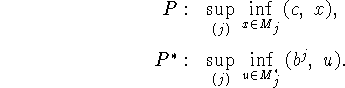
Условия одновременной разрешимости P и 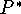 определяются
теоремами и , но возможна и ситуация:
P не разрешима,
определяются
теоремами и , но возможна и ситуация:
P не разрешима,  разрешима. Это соответствует тому, что
при разрешимости
разрешима. Это соответствует тому, что
при разрешимости 
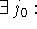
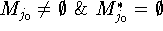 , т.е. задача
, т.е. задача 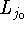 - несобственная 2-го
рода. Так как в рассматриваемой ситуации
- несобственная 2-го
рода. Так как в рассматриваемой ситуации 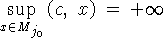 , то opt
, то opt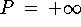 ,
т.е. P не разрешима. Одновременная неразрешимость задач P и
,
т.е. P не разрешима. Одновременная неразрешимость задач P и
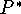 реализуется на паре задач линейного программирования L и
реализуется на паре задач линейного программирования L и
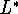 , являющихся несобственными 3-го рода [9, § 1].
, являющихся несобственными 3-го рода [9, § 1].
Конструкция двойственной задачи 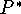 в форме (4.6)
подсказывается понятными соображениями, исходящими из двойственного
перехода
в форме (4.6)
подсказывается понятными соображениями, исходящими из двойственного
перехода 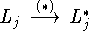 и необходимости
выполнения главного свойства теорем двойственности в МП, а именно:
optP=opt
и необходимости
выполнения главного свойства теорем двойственности в МП, а именно:
optP=opt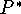 . Для обеспечения последнего соотношения
в
. Для обеспечения последнего соотношения
в 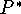 и введена операция
и введена операция 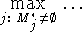 , хотя соображения симметрии требуют в двойственной
задаче иметь общую операцию
, хотя соображения симметрии требуют в двойственной
задаче иметь общую операцию 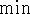 (как в исходной присутствует
(как в исходной присутствует
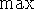 ). В этом смысле конструкция задачи
). В этом смысле конструкция задачи 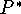 выглядит
несколько искусственной. Здесь возможен несколько другой подход. Он
связан с известным генеральным положением относительно
двойственности, когда исходная задача записывается через свой
эквивалент в форме максимина функции Лагранжа, а тогда минимакс этой
функции объявляется объектом, двойственным к исходному. Для задач
линейного программирования это и приводит к классической
двойственности. Для пояснения можно привести схему:
выглядит
несколько искусственной. Здесь возможен несколько другой подход. Он
связан с известным генеральным положением относительно
двойственности, когда исходная задача записывается через свой
эквивалент в форме максимина функции Лагранжа, а тогда минимакс этой
функции объявляется объектом, двойственным к исходному. Для задач
линейного программирования это и приводит к классической
двойственности. Для пояснения можно привести схему:
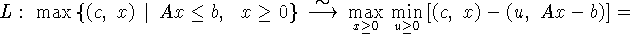
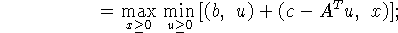
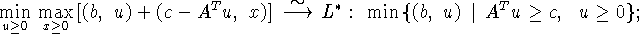
здесь символ  означает эквивалентный переход.
означает эквивалентный переход.
Оказывается, что как и в классическом случае, максимин
дизъюнктивной функции Лагранжа, т.е. 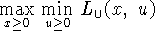 , эквивалентен исходной
задаче, которой для нас является (4.1) (она обозначена символом
P), а минимакс этой функции, т.е.
, эквивалентен исходной
задаче, которой для нас является (4.1) (она обозначена символом
P), а минимакс этой функции, т.е. 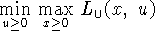 , эквивалентен как раз
задаче (4.6), что будет показано ниже. Задачи (4.1) и
(4.6) допускают эквивалентную перезапись:
, эквивалентен как раз
задаче (4.6), что будет показано ниже. Задачи (4.1) и
(4.6) допускают эквивалентную перезапись:
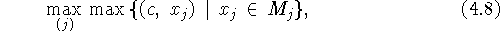
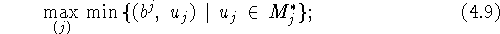
здесь 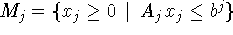 ,
,
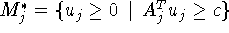 .
Прежде чем установить эквивалентности
.
Прежде чем установить эквивалентности
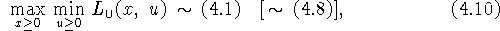
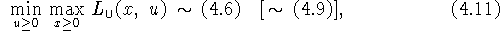
докажем вспомогательное утверждение. Запишем задачу
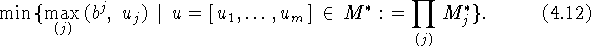
Лемма 4.1. Задачи 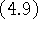 и
и 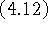 эквивалентны в смысле
эквивалентны в смысле
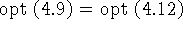 и 1) если
и 1) если
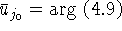 , то
, то 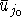 является
является
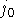 -ой координатой некоторого оптимального вектора
-ой координатой некоторого оптимального вектора 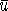 задачи
задачи 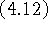 , и обратно 2) если
, и обратно 2) если 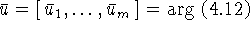 ,
,
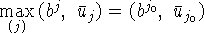 ,
то
,
то 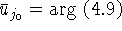 .
.
Д о к а з а т е л ь с т в о. Пусть 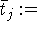 opt
opt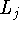 (=opt
(=opt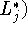 ,
, 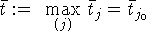 . Очевидно,
. Очевидно, 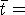 opt(4.9).
Задачу (4.12) можно переписать в эквивалентном виде
opt(4.9).
Задачу (4.12) можно переписать в эквивалентном виде
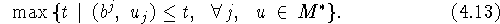
Значение 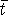 (=opt(4.9)) неуменьшаемо
в (4.13), так как оно неуменьшаемо в задаче
(=opt(4.9)) неуменьшаемо
в (4.13), так как оно неуменьшаемо в задаче 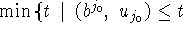 ,
, 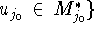 . Это и
дает равенство opt(4.9)=opt(4.12). Свойства 1) и
2) из формулировки леммы вытекают из конструкции рассматриваемой пары
задач.
. Это и
дает равенство opt(4.9)=opt(4.12). Свойства 1) и
2) из формулировки леммы вытекают из конструкции рассматриваемой пары
задач.
Теорема 4.5. Пусть задача 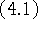 разрешима и вполне регулярна, т.е.
разрешима и вполне регулярна, т.е.
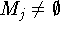 ,
, 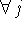 . Тогда
. Тогда
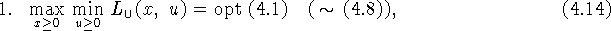
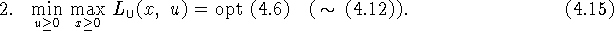
Д о к а з а т е л ь с т в о. 1. Рассмотрим внутреннюю операцию в левой
части (4.14):
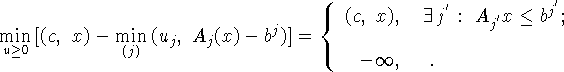
Выписанное равенство не нуждается в особом обосновании, из него
и следует соотношение:
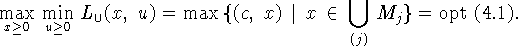
2. Выпишем внутреннюю операцию в левой части (4.15),
преобразовав очевидным образом функцию 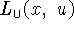 :
:
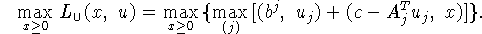
Отсюда следует
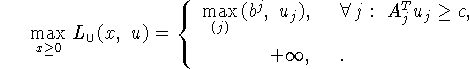
Полученное соотношение дает
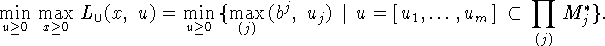
Задача, стоящая в правой части полученного равенства, по
лемме эквивалентна задаче (4.9), т.е.
задаче (4.6), двойственной к (4.1). Теорема доказана.
З а м е ч а н и е 4.2.
На самом деле равенство из п. 1 имеет место для общей постановки
задачи дизъюнктивного программирования (4) и ее дизъюнктивной
функции Лагранжа (6). Проверка этого аналогична предыдущему
обоснованию.
4.4. Симметричная постановка задач (4.1) и (4.6),
находящихся в двойственности
Задача (4.1), к которой сводится любая задача
кусочно-линейного программирования, распадается на конечное число
параллельных задач
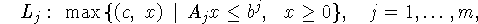
оптимальные значения которых и формируют оптимальное значение
задачи (4.1): opt(4.1)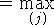 opt
opt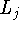 .
Очевидным обобщением этой постановки является задача
.
Очевидным обобщением этой постановки является задача
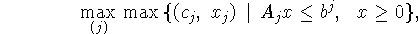
которую можно записать в эквивалентном виде:
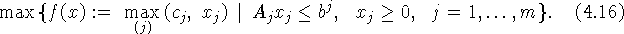
В качестве двойственной к ней, согласно примененной выше схеме,
выступает задача
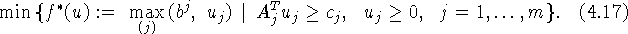
Эти задачи (в предположении разрешимости 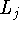 ,
, 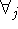 )
связаны классическими соотношениями двойственности:
)
связаны классическими соотношениями двойственности:
-
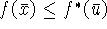 для допустимых
для допустимых 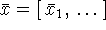 и
и 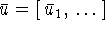 ;
;
- opt(4.16)=opt(4.17).
В аналогичных соотношениях двойственности находится и пара
задач, получающаяся заменой 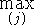 в (4.16)
на
в (4.16)
на 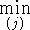 :
:
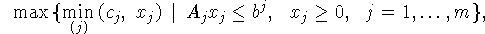
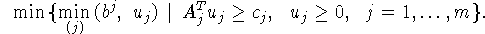
Отметим, что при рассмотрении двойственности в
кусочно-линейном программировании в качестве
самостоятельной выступает операция
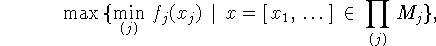
где 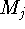 - множество из пространства переменной
- множество из пространства переменной 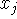 .
Через этот тип оптимизационной операции
выражается как исходная задача
.
Через этот тип оптимизационной операции
выражается как исходная задача
 -кусочного программирования, так и
формируемая для них двойственность.
-кусочного программирования, так и
формируемая для них двойственность.
Заметим также, что отмеченное свойство  для допустимых x и u позволяет решение задач (4.1) и
(4.6) редуцировать к решению системы кусочно-линейных неравенств
для допустимых x и u позволяет решение задач (4.1) и
(4.6) редуцировать к решению системы кусочно-линейных неравенств
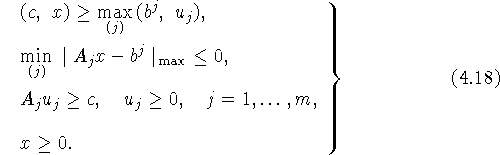
Связь между задачами (4.1), (4.6) и (4.18)
очевидная:
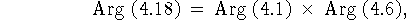
здесь символ Arg(4.18) означает множество решений
системы (4.18), которая является аналогом системы: 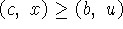 ,
, 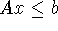 ,
, 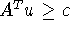 ,
, 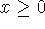 ,
, 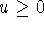 для
задачи ЛП:
для
задачи ЛП:
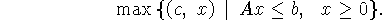


Next: Двойственность для несобственных
Up: СИГМА-КУСОЧНЫЕ ФУНКЦИИ И ЗАДАЧИ
Previous: Кусочно-линейные функции
и