7. Методы Рунге-Кутта с интерполяцией и экстраполяцией предыстории многочленами k-й степени

В этом разделе предполагаем, что x(t) - точное решение системы (1.1) является k+1 раз непрерывно дифференцируемым на отрезке .

При достаточно малых разобьем отрезок справа на отрезки , , длиной таким образом, что , , .... На каждом отрезке построим интерполяционный многочлен по данным , ,..., [16, c. 127,]:

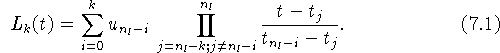
При всех справедливо

где

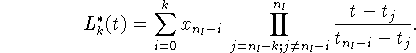
Тогда погрешность интерполяции точного решения вычисляется по формуле [16, c. 133,]

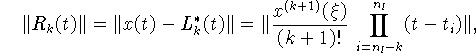
где . Таким образом, если , то

где . Кроме того, имеем оценку



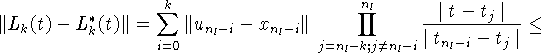
Из (7.2) и (7.3) получаем

где , .

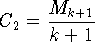Аналогично, если , то построив интерполяционный многочлен k-й степени по данным , ,..., имеем при экстраполяции

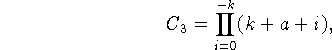
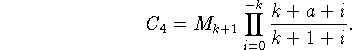
Опишем модификацию метода Рунге-Кутта (2.1) - (2.3), в которой интерполяция предыстории модели на отрезке и экстраполяция предыстории на отрезке производится многочленами k-й степени. Пусть

Функция при продолжена вправо от построенным на многочленом :

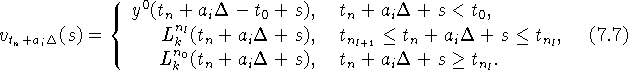
Если , то при построении интерполяционного многочлена на отрезке вместо тех значений интерполируемой модели в точках , где i < 0, нужно брать известные значения функции-предыстории точного решения .

Теорема 7.1. Если решение x(t) является (k+1)-раз непрерывно дифференцируемым на отрезке , то порядок сходимости метода (2.1) - (2.3), (7.6), (7.7) не меньше минимума из k+1 и l, где l - порядок аппроксимации метода.

Доказательство теоремы аналогично доказательствам теорем 3.1 и 6.1 со следующими изменениями в оценках и обозначениях:

Замечание 7.1. Методы, описанные в разделах 3 и 6 не являются частными случаями метода, описанного в этом разделе. Так, например, в методе раздела 6 экстраполяция предыстории модели проводится не многочленом первой степени, а непрерывным методом Рунге-Кутта низшего порядка (методом Эйлера).