8. Многошаговые методы

Наряду с методами типа Рунге-Кутта при решении ОДУ самыми распространенными являются многошаговые линейные методы, в частности методы типа Адамса.

При описании многошаговых методов для ФДУ будем использовать в основном те же обозначения, что и в разделе 2.

Пусть m - натуральное число, введем временной шаг и разобьем отрезок точками < < < < < < на отрезки длиной для ( считаем, что - целое число ).

Введем дискретную численную модель системы (1.1) - (1.3), обозначив приближения решения в точке через , где .

Из (1.2) - (1.3) получаем



В момент времени , где , для подсчета требуется интерполяция предыстории дискретной модели , , на отрезок .

Оператором интерполирования I предыстории модели назовем отображение

Здесь .

Для неявных методов потребуется также экстраполяция дискретной предыстории модели на полуинтервал .

Оператором экстраполирования E предыстории модели назовем отображение

Будем говорить, что интерполяция предыстории модели имеет порядок погрешности p, если найдутся и такие, что для всех и выполняется

Будем говорить, что экстраполяция предыстории модели имеет порядок погрешности p, если найдутся и такие, что для всех и выполняется

Некоторые конкретные способы интерполяции и экстраполяции были указаны выше. Далее будем считать операторы интерполяции I и экстраполяции E заданными.

Явным k-шаговым методом назовем дискретную модель вида

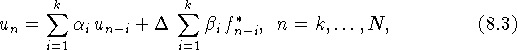
где и () - параметры метода, .

Неявным k-шаговым методом назовем модель

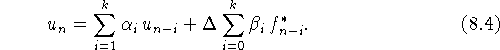
Отметим, что для применения моделей (8.3) или (8.4) при , необходимо знание стартовых значений , , которые определяют , (разгон). Будем говорить, что задан разгон порядка p, если найдется , такое, что для .

Для оценки погрешности метода введем величину и подставим , , в (8.4). Получим

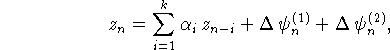
где

,


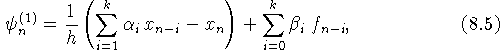
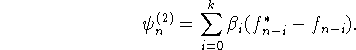
Величину будем называть погрешность аппроксимации многошагового метода (невязкой) и будем говорить, что погрешность аппроксимации имеет порядок p, если найдется такое, что для всех .

Будем говорить, что метод (8.4) сходится, если при для всех n=0,...,N, и имеет порядок сходимости p, если найдется C такое, что для всех .

Будем говорить, что метод (8.4) 0-устойчив, если выполняется условие корней [24], т.е. все корни производящего многочлена

удовлетворяют условию , причем, если то корень простой.

Теорема 8.1. Пусть многошаговый метод (8.4) 0-устойчив и имеет
1) порядок погрешности аппроксимации ,
2) разгон порядка ,
3) порядок интерполяции предыстории модели ,
4) порядок экстраполяции предыстории модели .
Тогда он сходится, причем порядок сходимости , , , .

Теорема доказывается стандартными методами [24, 16, 36, 17].