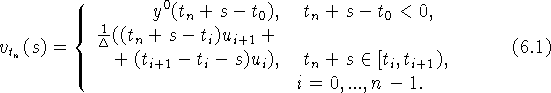
Таким образом
Согласно теореме 3.1 порядок сходимости методов Рунге-Кутта (2.1) - (2.3) при кусочно-постоянной интерполяции (2.4) и экстраполяции (2.5) определяется не только порядком аппроксимации метода, но и порядком модуля непрерывности точного решения. Даже если точное решение достаточно гладкое, например, выполняется условие 4.1, то модуль непрерывности имеет первый порядок и, поэтому, это обеспечивает лишь первый порядок сходимости при любом порядке аппроксимации метода (2.1) - (2.3). Ниже приводится модификация метода Рунге-Кутта, обеспечивающая второй порядок сходимости (при условии, что порядок аппроксимации метода (2.1) - (2.3) не ниже второго).
Введем функцию ![]() ,
, ![]() , кусочно-линейную при
, кусочно-линейную при
![]() :
:
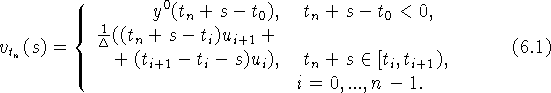
Таким образом ![]() , если
, если ![]() ,
, ![]() ,
а между точками
,
а между точками ![]() проведена линейная интерполяция при
проведена линейная интерполяция при ![]() .
.
Функция ![]() при
при ![]() продолжена вправо (проведена экстраполяция за точку
продолжена вправо (проведена экстраполяция за точку ![]() ) по методу
Эйлера:
) по методу
Эйлера:
![]()
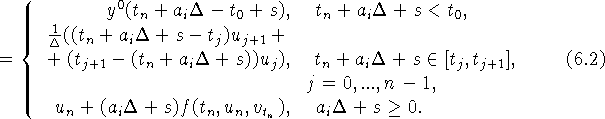
Заметим, что в отличие от (2.4), (2.5) функция ![]() в (6.1) - (6.2) является непрерывной.
в (6.1) - (6.2) является непрерывной.
Теорема 6.1.
Пусть решение x(t) дважды непрерывно дифференцируемо
на ![]() , тогда если метод (2.1) - (2.3) ,
(6.1), (6.2) имеет порядок аппроксимации l, то он сходится,
причем порядок сходимости не меньше минимума из l и 2.
, тогда если метод (2.1) - (2.3) ,
(6.1), (6.2) имеет порядок аппроксимации l, то он сходится,
причем порядок сходимости не меньше минимума из l и 2.
Доказательство теоремы в основном повторяет доказательство теоремы 3.1, поэтому укажем лишь отличия.
В силу линейной интерполяции (6.1) имеем при ![]() ,
k=1,...,n,
,
k=1,...,n,
![]()
где ![]() .
.
Тогда вместо оценки (3.12) имеем оценку
![]()
Для получения аналога оценки (3.14) проведем оценку
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Поэтому, вместо (3.13) имеем
![]()
и оценка (3.14) справедлива при так определенном ![]() .
.
Вместо (3.18) имеем
![]()
а вместо (3.19) получаем
![]()
где
![]()
![]()
![]()
Далее теорема 6.1 доказывается как и теорема 3.1, только вместо ![]() из (3.21) нужно взять
из (3.21) нужно взять
![]()
Замечание 6.1. Теорема 6.1 справедлива также, если точное решение
x(t) дважды непрерывно дифференцируемо не на всем отрезке
![]() ,
а лишь на полуинтервалах
,
а лишь на полуинтервалах ![]() ,
, ![]() при
n=0,...,N-1.
при
n=0,...,N-1.
Замечание 6.2. Интерполяцию предыстории модели (6.1) и ее экстраполяцию (6.2) имеет смысл применять, когда используется метод Рунге-Кутта второго порядка аппроксимации (см. раздел 5). В этом случае общий порядок сходимости равен 2. Экстраполяция предыстории модели по методу Эйлера (6.2) играет роль прогноза, а роль коррекции играет сам метод Рунге-Кутта второго порядка.