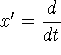Рассмотрим систему с ограниченным последействием
и начальными условиями
Здесь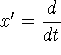 
,
,
- величина интервала запаздывания,
, 
,
- l-мерное евклидово пространство со
скалярным произведением 
и нормой
;
- пространство l-мерных кусочно-непрерывных на
функций 
с нормой
.
Система (1.1) рассматривается в фазовом пространстве
, элементами которого являются пары
, а норма задается формулой
В дальнейшем предполагаем выполненным
Условие 1.1. Отображение 
является
непрерывным по сдвигу [10] в области определения и для
всех 
, 
и 
выполняется условие Липшица
Условие 1.1 гарантирует существование и единственность
кусочно-гладкого решения задачи Коши (1.1) - (1.3)
на интервале
[10].