Зададим на интервале 
временную сетку
, n = 0,1,...,N,
с равномерным шагом 
.
Введем численную модель системы (1.1), обозначив
приближение решения x(t) через 
.
Срезки функций x(t) и u(t) на полуинтервал 
будем обозначать
и
,
соответственно.
Будем также использовать обозначения 
,
, 
, 
,
, 
, 
, 
.
Для натурального m назовем m-этапным методом Рунге-Кутта
( с кусочно-постоянной интерполяцией и экстраполяцией предыстории)
численную модель вида
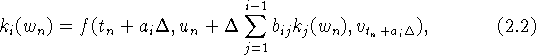
здесь 
,
, 
- параметры метода,
функция-предыстория 
при 
кусочно-постоянна
(интерполяция):
функция-предыстория 
при
продолжена вправо
(экстраполяция) постоянным вектором, равным 
:
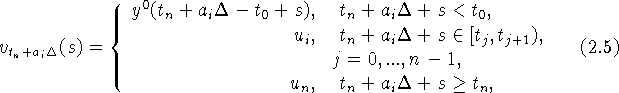
Заметим, что необходимая в методах (2.1) - (2.3)
интерполяция (2.4) и экстраполяция (2.5) функции-предыстории
модели 
проводится простейшим методом, требующим минимального
объема вычислений и памяти.
Далее будут рассмотрены более точные способы интерполяции и экстраполяции
функции .