Специфика ФДУ состоит в том, что изначально известны из (8.1) -
(8.2) значения модели ![]() при
при ![]() .
Однако применять формулы (8.3) - (8.4) без разгона, т.е. при
.
Однако применять формулы (8.3) - (8.4) без разгона, т.е. при
![]() , вообще говоря, нельзя, т.к. не определены значения
, вообще говоря, нельзя, т.к. не определены значения
![]() при i < 0.
при i < 0.
Если ![]() , то явням k-шаговым методом, не требующим разгона
назовем модель
, то явням k-шаговым методом, не требующим разгона
назовем модель
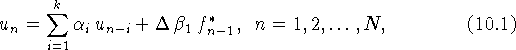
где ![]() при
при ![]() определяются из (8.1)-(8.2).
определяются из (8.1)-(8.2).
Как следует из (9.1), погрешность аппроксимации p метода
(10.1) удовлетворяет условию ![]() .
0-Устойчивыми методами (6.1), для которых p=k, являются :
.
0-Устойчивыми методами (6.1), для которых p=k, являются :
явный метод Эйлера
![]()
и правило средней точки
![]()
При ![]() среди методов вида (10.1), для которых p=k,
нет 0-устойчивых.
Однако существуют явные четырехшаговые 0-устойчивые методы третьего
порядка аппроксимации не требующие разгона, например метод
среди методов вида (10.1), для которых p=k,
нет 0-устойчивых.
Однако существуют явные четырехшаговые 0-устойчивые методы третьего
порядка аппроксимации не требующие разгона, например метод
![]()
При ![]() неявным k-шаговым методом, не требующим разгона,
назовем модель
неявным k-шаговым методом, не требующим разгона,
назовем модель
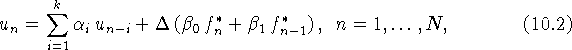
где ![]() при
при ![]() определно из (8.1), (8.2).
определно из (8.1), (8.2).
Из (9.1) следует, что порядок погрешности аппроксимации p
метода (10.2) удовлетворяет условию ![]() .
.
Среди методов вида (6.2), для которых p=k+1, 0-устойчивым
является лишь метод трапеций
![]()
Среди методов вида (10.2) для которых p=k, отметим формулы
дифференцирования назад (ФДН)
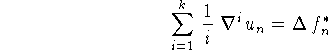
(здесь ![]() означает разность назад:
означает разность назад:
![]() ,
,
![]() ),
0-устойчивые при
),
0-устойчивые при ![]() [36].
[36].