 (1.1), обладающее достаточной гладкостью.
Предположим, что мы нашли решение на некотором интервале
(1.1), обладающее достаточной гладкостью.
Предположим, что мы нашли решение на некотором интервале 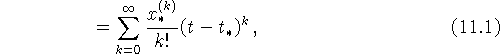
здесь
Следует отметить, что с вычислительной точки зрения применение рядов Тейлора не представляет практического интереса для нахождения приближенных решений даже в случае обыкновенных дифференциальных уравнений. Однако, этот подход используется как некоторый теоретический эталон, для сравнения с другими практически удобными методами.
Пусть x(t) - решение уравнения
 (1.1), обладающее достаточной гладкостью.
Предположим, что мы нашли решение на некотором интервале
(1.1), обладающее достаточной гладкостью.
Предположим, что мы нашли решение на некотором интервале ![]() .
Рассмотрим разложение этого решения в ряд Тейлора в правой
окрестности точки
.
Рассмотрим разложение этого решения в ряд Тейлора в правой
окрестности точки ![]()
![]()
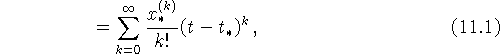
здесь ![]() (k=1,2,...) -
k-я производная решения в точке
(k=1,2,...) -
k-я производная решения в точке ![]() .
.
Если зафиксировать некоторое натуральное число N, то отрезок ряда
(11.1) :
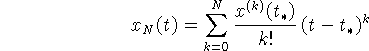
является приближенным решением задачи (1.1) - (1.3)
в некоторой окрестности точки ![]() (если мы сможем вычислить значения
(если мы сможем вычислить значения ![]() .
.
Опишем процедуру последовательного вычисления значений
![]() , k=0,1,...,N.
При этом будем предполагать существование всех необходимых производных и
использовать следующие обозначения :
, k=0,1,...,N.
При этом будем предполагать существование всех необходимых производных и
использовать следующие обозначения :
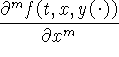 -- m-я частная производная по x,
-- m-я частная производная по x,
![]() -- m-я частная
коинвариантная производная по t.
-- m-я частная
коинвариантная производная по t.
1) Подставляя в уравнение (1.1) ![]() получаем формулу для
вычисления
получаем формулу для
вычисления ![]() :
:
![]()
2) Для нахождения ![]() продифференцируем обе части
уравнения (1.1) :
продифференцируем обе части
уравнения (1.1) :
![]()
![]()
Подставляя в (11.3) ![]() получим формулу для вычисления
получим формулу для вычисления ![]() .
.
3) Для нахождения ![]() продифференцировав обе части
уравнения (11.3) получаем :
продифференцировав обе части
уравнения (11.3) получаем :
![]()
![]()
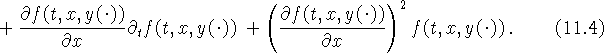
Подставляя в (11.4) ![]() получим формулу для вычисления
получим формулу для вычисления ![]() .
.
4) Продолжая далее последовательное дифференцирование получаемых
соотношений, можно вычислить
![]() ,
, ![]() ,...,
,...,![]() (см. далее замечание 11.2).
(см. далее замечание 11.2).
Замечание 11.1. Напомним, что если функционал ![]() имеет частную производную
имеет частную производную ![]() и инвариантную производную
и инвариантную производную ![]() , то коинвариантная производная
, то коинвариантная производная
![]() равна
равна
![]()
Замечание 11.2. Для k-ой производной ![]() решения уравнения
(1.1) в общем случае справедлива формула
решения уравнения
(1.1) в общем случае справедлива формула
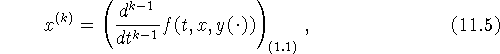
где
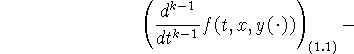
(k-1)-я полная производная функционала f в силу системы (1.1).
Для существования этой полной производной достаточно, чтобы все производные
функционала f по переменным t, x, ![]() до (k-1)-го порядка
были инвариантно непрерывны.
до (k-1)-го порядка
были инвариантно непрерывны.