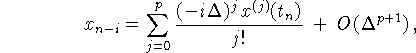
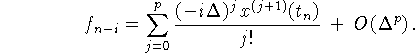
Подставив эти выражения в невязку (8.5) получаем, что порядок погрешности аппроксимации метода (8.4) не меньше

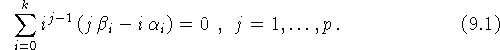
Отсюда следует, что порядок аппроксимации для неявных методов
Пусть точное решение задачи (1.1) - (1.3)
![]() .
Из формулы Тейлора имеем
.
Из формулы Тейлора имеем
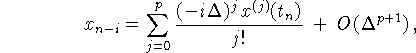
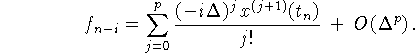
Подставив эти выражения в невязку (8.5) получаем, что порядок
погрешности аппроксимации метода (8.4) не меньше ![]() ,
если выполняются условия
,
если выполняются условия

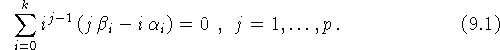
Отсюда следует, что порядок аппроксимации для неявных методов
![]() , для явных методов
, для явных методов ![]() .
.
Однако, как и для ОДУ [24], для 0-устойчивых k-шаговых методов
выполняются барьеры Далквиста:
1) ![]() для четных k,
для четных k,
2) ![]() для нечетных k,
для нечетных k,
3) ![]() если
если ![]() (в частности, для явных методов).
(в частности, для явных методов).
Для методов Адамса
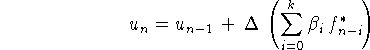
порядок погрешности аппроксимации ![]() для неявных методов и
для неявных методов и
![]() для явных.
для явных.
Разгон в k-шаговых методах можно делать методами типа Рунге-Кутта соответствующего порядка.