6. Устойчивость оптимального синтеза

Предположим, что сигналы обратной связи, доставляющие в регулятор информацию о реализовавшихся на деле значениях фазового вектора $x$ в каждый текущий момент времени $k,$ сопровождаются помехами $p(k),$ и возмущенное движение $y(k)$ управляемого объекта является решением системы первых разностей

$$y(k+1)=A y(k)+B u^0\bigl[k, y(k)+p(k)\bigr]$$ (6.1)

при начальном условии

$$y(k_0)=x_0+p(k_0).$$ (6.2)

О п р е д е л е н и е 6.1. Оптимальный синтез $u^0(k, x)$ устойчив при постоянно действующих возмущениях, если для любого $\varepsilon>0$ можно указать $\delta=\delta(\varepsilon)>0$ такое, что возмущенное движение $y(k)$ системы (6.1), порождаемое начальным условием (6.2), при всех $k$ таких, что $k_0\le k \le N$, удовлетворяет неравенству

$$\Vert y(k)-x^0(k)\Vert<\varepsilon,$$ (6.3)

если только

$$\Vert p(k)\Vert<\delta \qquad (k_0\le k\le N-1).$$ (6.4)

Изучим свойства оптимальной системы

$$x^0\bigl[k+1\bigr]=A x^0[k]+B u^0(k, x) ,$$

которую, учитывая (3.3), можем записать в виде

$$x^0(k+1)=Ax^0(k)+BS^T(k){\cal D}^+(k) c(k).$$ (6.5)

Уравнения возмущенного движения, отвечающие (6.1), имеют вид

$$y(k+1)=Ay(k)+BS^T(k){\cal D}^+(k)\Bigl(x_1-A^{N-k}\bigl(y(k)+p(k)\bigr)\Bigr),$$

откуда

$$y(k+1)=Ay(k)+BS^T(k){\cal D}^+(k)\left(x_1-A^{N-k}y(k)\right) - BS^T(k){\cal D}^+(k)A^{N-k}p(k).$$

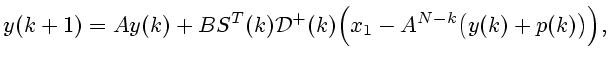
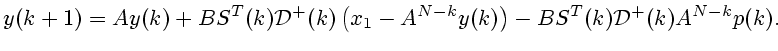
Далее используем метод математической индукции.

База индукции. При $k=k_0$ имеем $\Vert y(k_0)-x^0(k_0)\Vert=\Vert p(k_0)\Vert,$ и достаточно взять $\delta(\varepsilon)=\varepsilon.$ Рассмотрим $k=k_0+1.$ Решения невозмущенной (6.5) и возмущенной (6.1) систем при начальных условиях соответственно $x(k_0)=x_0$ и (6.2) принимают вид

$$x^0(k_0+1)= Ax_0+BS^T(k_0){\cal D}^+(k_0)\left(x_1-A^{N-k_0}x_0\right),$$

$$y^0(k_0+1)= Ay(k_0)+BS^T(k_0){\cal D}^+(k_0)\left(x_1-A^{N-k_0}y(k_0)\right)=$$

$$=Ax_0+Ap(k_0)+ BS^T(k_0){\cal D}^+(k_0)\left(x_1-A^{N-k_0}x_0\right)-$$

$$-BS^T(k_0){\cal D}^+(k_0)A^{N-k_0}p(k_0),$$

откуда находим

$$y^0(k_0+1)-x^0(k_0+1)= \left(A-BS^T(k_0){\cal D}^+(k_0)A^{N-k_0}\right)p(k_0).$$

Обозначим для краткости

$$A-BS^T(k_0){\cal D}^+(k_0)A^{N-k_0}=F(k_0);$$

тогда

$$\bigl\Vert y(k_0+1)-x^0(k_0+1)\bigr\Vert \le \bigl\Vert F(k_0)\bigr\Vert\cdot \bigl\Vert p(k_0)\bigr\Vert,$$ (6.6)

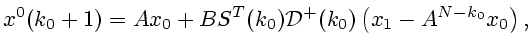
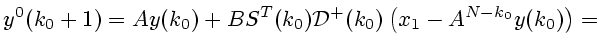
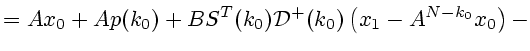
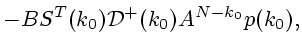
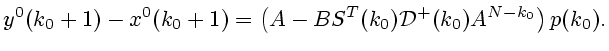
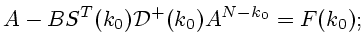
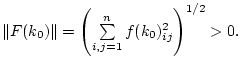где $\Vert F(k_0)\Vert=\left( \sum\limits_{i,j=1}^n f(k_0)_{ij}^2\right)^{1/2}>0.$ Полагая теперь $\delta=\varepsilon/\Vert F(k_0)\Vert,$ получаем из (6.6): $\Vert y(k_0+1)-x^0(k_0+1)\Vert\le \varepsilon,$ т.е. при $k=k_0+1$ устойчивость доказана.

Шаг индукции. Будем считать, что для всех $k$ таких, что $k_0\le k\le q< N,$ предположение индукции об устойчивости оптимального синтеза $u^0(k, x)$ верно. Докажем его справедливость для $k=q+1.$ Из предыдущих рассуждений получаем, что

$$y(q+1)-x^0(q+1)=A\left(y(q)-x^0(q)\right)-BS^T(q){\cal D}^+(q)\times {}$$

$${} \times A^{N-q}\left(y(q)-x^0(q)\right)-BS^T(q){\cal D}^+(q)A^{N-q} p(q),$$

откуда

$$\begin{array}{c} \bigl\Vert y(q+1)-x^0(q+1)\bigr\Vert \le ... ...rt F_1(q)\bigr\Vert\cdot \bigl\Vert p(q)\bigr\Vert, \end{array}$$ (6.7)

где $F_1(q)=BS^T(q){\cal D}^+(q)A^{N-q}.$ В силу предположения индукции, при $k = q$ для любого $\bar\varepsilon>0$ существует $\delta(\bar\varepsilon)>0$ такое, что из неравенства $\Vert p(l)\Vert<\delta(\bar\varepsilon)$ для всех $l=k_0, k_0+1,\ldots,q-1$ следует $\Vert y(q)-x^0(q)\Vert<\bar\varepsilon.$ Возьмем произвольное $\varepsilon>0$ и рассмотрим $\bar\varepsilon=\min \Bigl\{ \varepsilon/\left(3\Vert A\Vert\right),\ \varepsilon/\left(3\Vert F_1\Vert\right) \Bigr\},$ где $\Vert F_1\Vert=\max\limits_{k_0\le k\le N-1} \Vert F_1(k)\Vert>0$ и предполагается, что $\Vert A\Vert>0.$ Находим $\delta(\bar\varepsilon)$ и полагаем $\delta(\varepsilon)=\min\bigl\{ \delta(\bar\varepsilon), \varepsilon/\left(3\Vert F_1\Vert\right) \bigr\}.$ Тогда, учитывая (6.7), получаем требуемое неравенство $\Vert y(q+1)-x^0(q)\Vert<\Vert A\Vert \bar\varepsilon +\Vert F_1(q)\Vert \bar\varepsilon+\Vert F_1(q)\Vert\delta(\bar\varepsilon)<\varepsilon.$ Шаг индукции выполняется. Таким образом, доказана следующая

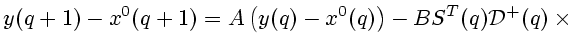
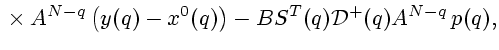
Теорема 6.1. Оптимальный синтез $u^0(k, x)=S^T(k){\cal D}^+(k) c(k), k=k_0, k_0+1,\ldots,N-1,$ устойчив при постоянно действующих возмущениях, ограниченных в каждый момент времени.

Следствие 6.1. При выполнении условий $(\ref{q64}), (\ref{q65})$ справедливо неравенство

$$\Bigl\Vert u^0(k, x)-u^0\bigl[k, p(k)\bigr]\Bigr\Vert<\varepsilon \quad (k_0\le k\le N-1),$$ (6.8)

где $u^0\bigl[k, p(k)\bigr]=u^0\bigl(k, y(k)+p(k)\bigr).$

Д о к а з а т е л ь с т в о. В самом деле, согласно (3.3), для системы (6.5)

$$u^0(k, x)=S^T(k){\cal D}^+(k) c(k)=S^T(k){\cal D}^+(k)\left(x_1-A^{N-k}x^0(k)\right).$$

Для возмущенной системы (6.1)

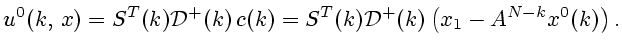
$$u^0\bigl[k, p(k)\bigr]=S^T(k){\cal D}^+(k)\Bigl(x_1-A^{N-k}\bigl(y(k)+p(k)\bigr)\Bigr)=$$

$${}=S^T(k){\cal D}^+(k)\left(x_1-A^{N-k}y(k)\right)-S^T(k){\cal D}^+(k)A^{N-k}p(k).$$

Обозначим

$$F_2(k)=S^T(k){\cal D}^+(k)A^{N-k} , \quad k=k_0,\ldots,N-1 ,$$

и пусть

$$\Vert F_2\Vert=\max\limits_{k_0\le k\le N-1} \Vert F_2(k)\Vert>0.$$

Тогда справедлива оценка

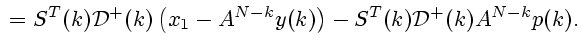
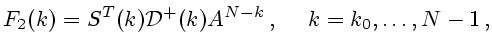
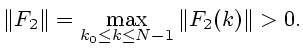
$$\Bigl\Vert u^0(k, x)-u^0\bigl[k, p(k)\bigr]\Bigr\Vert \le \Vert F_2\Vert\cdot\bigl(\Vert y(k)-x^0(k)\Vert+\Vert p(k)\Vert\bigr).$$

Возьмем произвольное $\varepsilon>0$ и рассмотрим $\bar\varepsilon=\ \varepsilon/\left(2\Vert F_2\Vert\right)>0.$ Тогда в силу теоремы 6.1 найдется $\delta(\bar\varepsilon)>0$ такое, что $\Vert y(k)-x^0(k)\Vert<\bar\varepsilon.$ Полагая $\delta(\varepsilon)=\min \Bigl\{ \delta(\bar\varepsilon), \ \varepsilon/\left(2\Vert F_2\Vert\right) \Bigr\},$ получим неравенство (6.8).

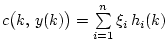З а м е ч а н и е. При $k_0\le k\le k^*,$ где $k^*$ введено в § 4, ранг матрицы $H^{(k)}$ равен $n,$ т.е. линейно независимые столбцы матрицы $H^{(k)}\ \linebreak h_1(k), h_2(k),\ldots,h_n(k)$ образуют базис в ${\Bbb R}^n.$ При этом вектор $c\bigl(k, y(k)\bigr)\in {\Bbb R}^n$ можно представить в виде $c\bigl(k, y(k)\bigr)=\sum\limits_{i=1}^n \xi_i h_i(k)$ и уравнение

$$H^{(k)}u^{(k)}=c\bigl(k, y(k)\bigr)$$ (6.9)

разрешимо. Следовательно, существует оптимальное управление $u^{0 (k)},$
приводящее систему (6.1) из $y(k)$ в заданное конечное состояние $x_1,$ если помеха $p(k)$ действует только при $k_0\le k\le k^*.$ Если же $k_0< k\le N-1,$ то уравнение (6.9) остается разрешимым, только если $c\bigl(k, y(k)\bigr)\in R^{r(k)}$, где $R^{r(k)}$ - подпространство, натянутое на линейно независимые векторы $h_1(k),\ldots$, $h_{r(k)}(k)$ матрицы $H^{(k)},$ $r(k)=$ rank $H^{(k)}<n.$ Иначе условие 2.1 нарушится и управление, решающее задачу 1.2, не существует. Но поскольку в обоих случаях реально действует управление $u^0\bigl[k, y(k)+p(k)\bigr],$ $k=k_0, k_0+1,\ldots,N-1,$ а не $u^0\bigl[k, y(k)\bigr],$ то при $p(k)\ne 0,\ k=k_0+1, k_0+2,\ldots,N-1,$ желаемое конечное состояние $x_1$ недостижимо. Выполняется лишь неравенство $\Vert y(N)-x_1\Vert<\varepsilon.$

Основные результаты.

Рассмотрена задача приведения линейной дискретной системы (1.1) в заданное конечное состояние $x_1$ при наличии квадратичного критерия качества (1.2). С использованием псевдообратной матрицы построено оптимальное программное управление $u^0(k)$ (2.10), решающее данную задачу. Также найдено решение задачи о синтезе в случае, когда оно существует и показано, что если решение не существует, то построенное согласно (3.3) управление $u^0\bigl[k; k, x^0(k)\bigr]$ приводит систему (1.1) так близко к $x_1,$ как только возможно.

Изучены свойства оптимального управления $u^0\bigl[k; k, x^0(k)\bigr].$ Доказано, что при определенных условиях справедливо равенство $D^+(k) c(k)=c=$const, $k=k_0, k_0+1,\ldots,N-1,$ являющееся аналогом первого интеграла в случае решения аналогичной задачи для системы дифференциальных уравнений.

Кроме того, показано, что при определенных условиях оптимальный синтез устойчив к помехам в каналах обратной связи, хотя при отличной от нуля помехе при $k=k_0+1, k_0+2,\ldots,N-1$ он переводит систему (1.1) лишь в заданную сколь угодно малую $\varepsilon$-окрестность точки $x_1.$