

Next: 3 Решение задачи о
Up: SAZ
Previous: 1 Постановка задачи
Введем обозначения
![\begin{displaymath}\begin{array}{c} c(k_0, x_0)=x_1-A^{N-k_0}x_0,\quad S(k)=A^{...
...0)}=\bigl[S(k_0), S(k_0+1),\ldots, S(N-1)\bigr] , \end{array}\end{displaymath}](img35.gif) |
(2.1) |
где матрица 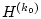 имеет размерность
имеет размерность
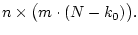 Предположим, что значения
Предположим, что значения 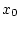 и
и 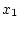 и момент времени
и момент времени 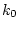 таковы, что
выполняется следующее
таковы, что
выполняется следующее
У с л о в и е 2.1. Вектор
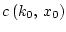 принадлежит подпространству,
натянутому на линейно независимые столбцы матрицы
принадлежит подпространству,
натянутому на линейно независимые столбцы матрицы
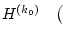 заметим, что
данное условие равносильно требованию полной управляемости систе-
заметим, что
данное условие равносильно требованию полной управляемости систе-
мы
1.1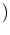 .
.
Тогда в обозначениях (2.1) справедливо
Утверждение 2.1. Для того чтобы управления
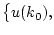
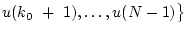 переводили систему (1.1) из состояния
переводили систему (1.1) из состояния
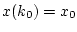 в
состояние
в
состояние
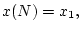 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 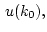
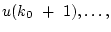
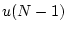 удовлетворяли матричному уравнению
удовлетворяли матричному уравнению
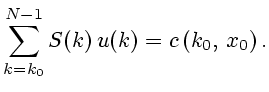 |
(2.2) |
Д о к а з а т е л ь с т в о.
Необходимость. Пусть управления 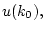
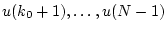 переводят систему (1.1) из состояния
переводят систему (1.1) из состояния 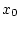 в состояние
в состояние 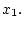 Тогда
справедливы соотношения
Тогда
справедливы соотношения
В правой части каждого уравнения заменим
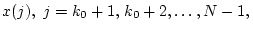 его выражением согласно
предыдущему уравнению; получим следующее равенство:
или, что то же,
Но
его выражением согласно
предыдущему уравнению; получим следующее равенство:
или, что то же,
Но
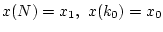 по условию; тогда, учитывая обозначения
(2.1), получаем: управления
по условию; тогда, учитывая обозначения
(2.1), получаем: управления 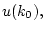
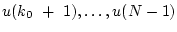 удовлетворяют уравнению
удовлетворяют уравнению
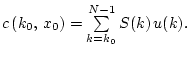
Достаточность. Пусть управления
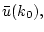
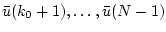 удовлетворяют уравнению (2.2) при
удовлетворяют уравнению (2.2) при
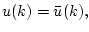
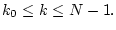 При заданных управлениях система (1.1) приходит в точку
При заданных управлениях система (1.1) приходит в точку
Поскольку начальное состояние есть
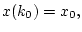 имеем
имеем
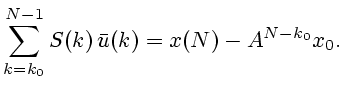 |
(2.3) |
Сравнивая правые части (2.2) при
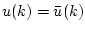 и (2.3), приходим
к равенству
откуда, используя (2.1), находим:
и (2.3), приходим
к равенству
откуда, используя (2.1), находим: 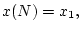 т.е. управления
т.е. управления
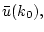
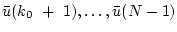 приводят систему (1.1) из
приводят систему (1.1) из
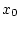 в
в 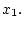 Утверждение доказано.
Утверждение доказано.
Далее рассмотрим вектор из 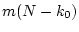 компонент
компонент
![$\displaystyle u^{(k_0)}= \left[ \begin{array}{c} u(k_0) \ [1ex] u(k_0+1) \ [1ex] \vdots \ [1ex] u(N-1) \end{array} \right].$](img75.gif) |
(2.4) |
Соотношение (2.2) тогда может быть представлено уравнением
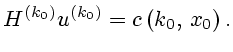 |
(2.5) |
Для построения решения задачи 1.1 или (что то же, в силу Утверждения
2.1) решения уравнения (2.5) с условием (1.2) введем в рассмотрение
псевдообратную матрицу
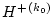 следующим ее представлением
следующим ее представлением
([8, стр. 33]):
Для краткости, учитывая определение
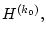 обозначим
обозначим
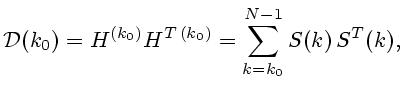 |
(2.6) |
где
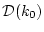 - симметрическая, неотрицательно определенная матрица
размерности
- симметрическая, неотрицательно определенная матрица
размерности
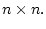 Для нее, согласно ([9, стр. 276]),
Для нее, согласно ([9, стр. 276]),
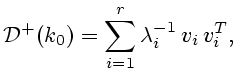 |
(2.7) |
где
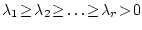 -
собственные числа
матрицы
-
собственные числа
матрицы
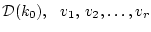 - отвечающие им
ортонормированные собственные векторы. Таким образом,
- отвечающие им
ортонормированные собственные векторы. Таким образом,
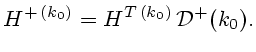 |
(2.8) |
В указанных обозначениях нормальное псевдорешение ([8, стр. 39])
уравнения (2.5) выражается формулой
или
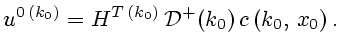 |
(2.9) |
Заметим, что относительно неизвестных 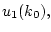
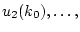
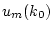 ,
,
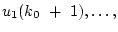
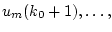
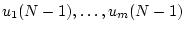 выражение (2.5)
представляет собой систему
выражение (2.5)
представляет собой систему 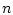 уравнений. При этом, как отмечалось в
[10,11],
уравнений. При этом, как отмечалось в
[10,11],
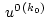 (2.9) совпадает с решением
системы
(2.5) с минимальной нормой в случае, если система совместна, и с
нормальным псевдорешением, если система несовместна.
(2.9) совпадает с решением
системы
(2.5) с минимальной нормой в случае, если система совместна, и с
нормальным псевдорешением, если система несовместна.
Взяв 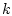 -ю компоненту вектора
-ю компоненту вектора
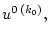 получаем оптимальное программное
управление
на
получаем оптимальное программное
управление
на 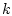 -м шаге,
-м шаге,
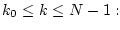
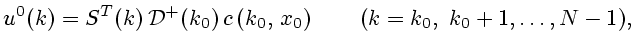 |
(2.10) |
которое далее будем обозначать
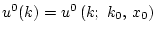 .
.
Отметим в заключение, что применительно к решению задач теории управления
псевдообратные матрицы использовались, в частности,
в ([4, стр. 124]).


Next: 3 Решение задачи о
Up: SAZ
Previous: 1 Постановка задачи
2003-08-29
![\begin{displaymath}\begin{array}{c} c(k_0, x_0)=x_1-A^{N-k_0}x_0,\quad S(k)=A^{...
...0)}=\bigl[S(k_0), S(k_0+1),\ldots, S(N-1)\bigr] , \end{array}\end{displaymath}](img35.gif)
![]() принадлежит подпространству,
натянутому на линейно независимые столбцы матрицы
принадлежит подпространству,
натянутому на линейно независимые столбцы матрицы
![]() заметим, что
данное условие равносильно требованию полной управляемости систе-
заметим, что
данное условие равносильно требованию полной управляемости систе-
![]() .
.
![]()
![]() переводили систему (1.1) из состояния
переводили систему (1.1) из состояния
![]() в
состояние
в
состояние
![]() необходимо и достаточно, чтобы
необходимо и достаточно, чтобы ![]()
![]()
![]() удовлетворяли матричному уравнению
удовлетворяли матричному уравнению
![]()
![]() переводят систему (1.1) из состояния
переводят систему (1.1) из состояния ![]() в состояние
в состояние ![]() Тогда
справедливы соотношения
Тогда
справедливы соотношения
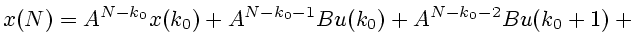
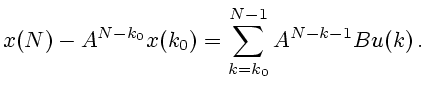
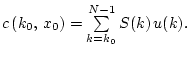
![]()
![]() удовлетворяют уравнению (2.2) при
удовлетворяют уравнению (2.2) при
![]()
![]() При заданных управлениях система (1.1) приходит в точку
При заданных управлениях система (1.1) приходит в точку
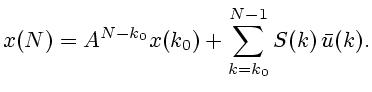
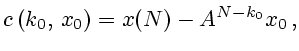
![]() компонент
компонент
![$\displaystyle H^{+ (k_0)}=H^{T (k_0)}\cdot \left[H^{(k_0)}H^{T (k_0)}\right]^+.
$](img78.gif)
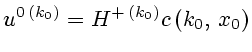
![]() -ю компоненту вектора
-ю компоненту вектора
![]() получаем оптимальное программное
управление
на
получаем оптимальное программное
управление
на ![]() -м шаге,
-м шаге,
![]()