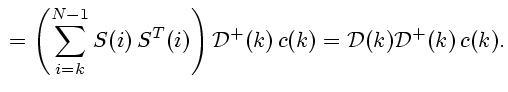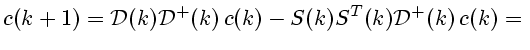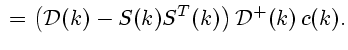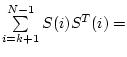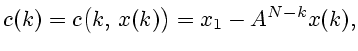 |
(3.1) |
Для решения задачи 1.2 введем обозначения
Теорема 3.1. Пусть выполнено условие 2.1, и
![]() - оптимальное программное управление, переводящее систему
- оптимальное программное управление, переводящее систему
![]() из состояния
из состояния
![]() в состояние
в состояние ![]() Тогда
Тогда
![]() и реализация управления, построенного по принципу обратной связи
и реализация управления, построенного по принципу обратной связи
![]() на оптимальном движении
на оптимальном движении ![]() совпадают,
т.е.
совпадают,
т.е.
Следовательно,
![]() (3.3) -
оптимальное управление, построенное по принципу обратной связи.
(3.3) -
оптимальное управление, построенное по принципу обратной связи.
Д о к а з а т е л ь с т в о. Доказательство проводим, пользуясь методом математической
индукции.
База индукции. Из (3.3) следует равенство (3.4) при
![]()
Шаг индукции. Пусть утверждение теоремы верно для всех ![]()
![]()
![]() Покажем, что оно выполняется и для
Покажем, что оно выполняется и для ![]() т.е. что
т.е. что
![\begin{displaymath}
u^{0 (q+1)}= \left[
\begin{array}{c}
u^0(q+1) \ [1ex]
u^0(q+2) \ [1ex]
\vdots \ [1ex]
u^0(N-1)
\end{array}\right],
\end{displaymath}](img121.gif)
В силу предположения индукции
![]() при
при
![]() значит, траектории,
соответствующие
обоим управлениям, до момента
значит, траектории,
соответствующие
обоим управлениям, до момента ![]() совпадают. В момент
совпадают. В момент ![]() движения
начинаются из одной и той же точки
движения
начинаются из одной и той же точки
![]() Следовательно,
Следовательно,
![]() представляет собой первые
представляет собой первые ![]() компонент
точного решения с минимальной нормой системы
компонент
точного решения с минимальной нормой системы
![]()
Допустим, что
![]() Тогда существуют два различных оптимальных управления с минимальной
нормой, переводящие систему (1.1) из
Тогда существуют два различных оптимальных управления с минимальной
нормой, переводящие систему (1.1) из ![]() в
в ![]() Первое -
программное, (2.9):
Первое -
программное, (2.9):
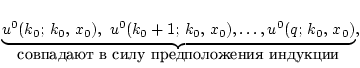
З а м е ч а н и е. Если при построении оптимального синтеза момент
времени ![]() достаточно близок к
достаточно близок к ![]() (для
(для ![]() ), то условие 2.1 для
заданных
), то условие 2.1 для
заданных ![]() и
и ![]() может не выполниться. При этом управление 3.4 не
приводит систему 1.1 в
может не выполниться. При этом управление 3.4 не
приводит систему 1.1 в ![]() , и задача 1.2 оказывается неразрешимой.
Подробнее эта ситуация обсуждается в § 5.
, и задача 1.2 оказывается неразрешимой.
Подробнее эта ситуация обсуждается в § 5.
Используя теорему 3.1, докажем вспомогательное утверждение, полезное при
дальнейшем анализе свойств оптимального управления (3.3).
Утверждение 3.1. Пусть выполнено условие ![]() Тогда для любого
Тогда для любого ![]() такого, что
такого, что
![]() справедливо равенство
справедливо равенство
Д о к а з а т е л ь с т в о. Рассмотрим разность
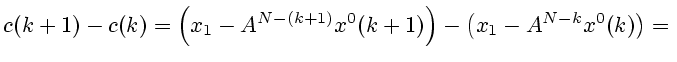
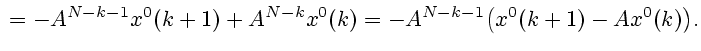
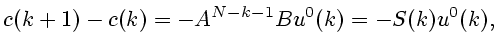
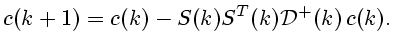
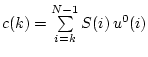 при
при ![$\displaystyle c(k)=\sum\limits_{i=k}^{N-1}S(i)\Bigl[S^T(i){\cal D}^+(k) c(k)\Bigr]={}
$](img165.gif)