3. Сходимость методов

Введем следующие обозначения: - погрешность, , .

Подставив величину в (2.1) получаем

Добавляя и вычитая в правой части этого соотношения величину
, получаем следующее уравнение для погрешности

где

Функцию , назовем невязкой или погрешностью аппроксимации метода (2.1) - (2.5).

Будем говорить, что:
1) метод (2.1) - (2.5) имеет порядок аппроксимации l, если для всех n=0,...,N ;
2) метод (2.1) - (2.5) сходится, если для всех n=1,...,N при и имеет порядок сходимости k, если для всех n=0,...,N.

Пусть - модуль непрерывности [9, с. 371,] функции x(t) на .

Будем говорить, что модуль непрерывности функции x(t) имеет порядок k, если .

Справедлива

Теорема 3.1. Если метод (2.1) - (2.5) имеет порядок аппроксимации l > 0, то он сходится, при этом порядок сходимости не меньше минимума из порядка аппроксимации и порядка модуля непрерывности точного решения и имеет место оценка

где









Доказательство . Для оценки величины в (3.3) оценим величину для i=1,...,m. Из (2.3) и Условия 1.1 следует

Для оценки при i>1 будем использовать следующие два свойства нормы пространства H: если x(t) непрерывная на функция, а , где продолжена вправо от постоянной, то



где ( - целая часть числа).

Оценим :







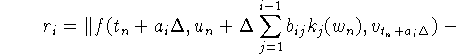
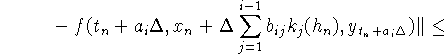
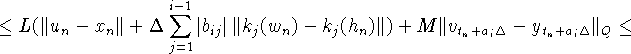
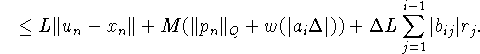
Обозначив

и учитывая (3.10), получаем

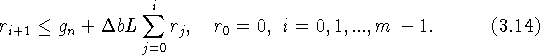
Учитывая оценку из [16, с. 222, лемма 1,] получаем

где

Из (3.15) и (3.3) следует оценка

Таким образом

Оценим погрешность . Из (3.1) и (3.18) следует

Обозначим

Докажем по индукции, что верна оценка

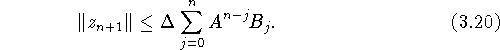
База индукции. Так как , , то из (3.19) следует

Шаг индукции. Пусть оценка (3.20) верна для , где . Покажем, что оценка справедлива и для .

Пусть максимум в правой части оценки (3.12) достигается на индексе , тогда и оценка (3.19) примет вид

Так как для n и индуктивное предположение выполняется, то





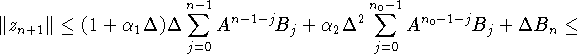
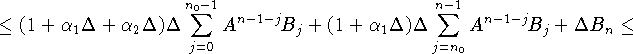
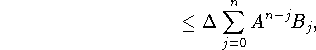
следовательно оценка (3.20) доказана.

Обозначим

тогда из (3.20) получаем оценку



из которой следует справедливость теоремы.