При m = 2 имеем семейство методов
где
Условие 5.1. Пусть параметры метода связаны соотношениями
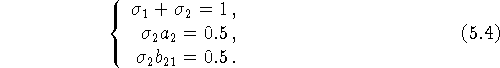
Условие 5.2. Решение x(t) системы (1.1) трижды
дифференцируемо на 
, причем третья производная
ограничена.
Условие 5.3. Отображение 
в правой части системы
(1.1) коинвариантно дифференцируемо в области определения
[10, c. 45,], причем для достаточно малых 
,
и всех 
где
,
.
Теорема 5.1. Если выполняются Условия 5.1 - 5.3, то порядок аппроксимации метода (5.1) - (5.3) равен 2.
Доказательство. Разложим x(t) по формуле Тейлора
и подставим в невязку
В силу (1.1) имеем
поэтому, в силу Условия 5.3, получаем
откуда, учитывая условие 5.1, следует справедливость утверждения 5.1.
В частности, условию 5.1 удовлетворяют методы
1) Эйлера с пересчетом
2) Коши
Порядок аппроксимации методов Рунге-Кутта при m>2 можно получить
аналогично, используя большую гладкость решении системы (1.1)
и понятия коинвариантных (или инвариантных) производных отображения
более высоких порядков.