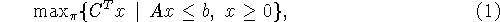
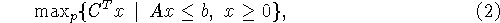
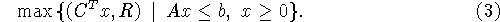
И. И. Еремин
Продолжены исследования по симметричной двойственности для линейных задач последовательной и Парето-последовательной оптимизации. В отличие от предшествующих работ автора здесь возможность неразрешимости исходных задач предполагается изначально. Намечены пути оптимальной аппроксимации несобственных задач отмеченных типов.
В работах [1, 2] автор рассматривал вопросы двойственности для задач лексикографического (последовательного) и Парето-последовательного программирования. Цель состояла в конструировании двойственности симметричной архитектуры, при этом исходная задача вместе с двойственной предполагались разрешимыми или, более общо, обладающими свойством собственности [1]. В работе [2] двойственность для несобственных задач линейной оптимизации рассматривалась через призму ее лексикографической интерпретации.
В данной работе рассматривается двойственность для задач паретовской и лексикографической оптимизации (Pareto-opt и lex-opt) без предположения их разрешимости, т.е. возможность неразрешимости (несобственности) исходной постановки предполагается изначально. Анализ ведется с позиций теории двойственности для несобственных задач математического программирования [3].
В (1) и (2) символы 
и 
означают соответственно паретовский и лексикографический максимум для
системы функций 
, 
(т.е. 
-
вектор-столбец) R - положительный k-мерный вектор-параметр.
Символ p в (2) будет в дальнейшем нести смысл упорядочения
функций , т.е. упорядочения номеров этих
функций, например, 
. Задачи (1) и (2)
сближают два обстоятельства: во-первых, имеет место включение
Arg(2)
Arg(1) - в случае их разрешимости
во-вторых, та и другая в определенном смысле редуцируются к
скаляризующей их задаче (3). В случае неразрешимости одной из них
связи между задачами (1) - (3) становятся более сложными.
Ниже рассматриваются вопросы симметричной двойственности (преимущественно) для задач (1) и (2) в случае их неразрешимости.
,
условия разрешимости