Из условий разрешимости задачи ЛП следуют условия разрешимости
задач ![]() и
и ![]() в следующих формах.
в следующих формах.
Пусть ![]() -
строчки матрицы A,
-
строчки матрицы A, ![]() - единичные орты пространства
R
- единичные орты пространства
R![]()
![]() - единичные орты пространства R
- единичные орты пространства R![]() . Выпишем
две группы соотношений:
. Выпишем
две группы соотношений:
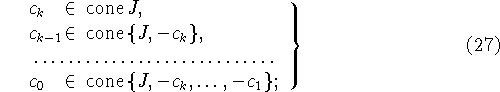
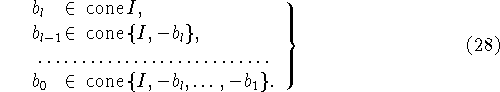
При ![]() разрешимость задачи
разрешимость задачи ![]() равносильна
выполнимости условий (27) при
равносильна
выполнимости условий (27) при ![]() разрешимость задачи
разрешимость задачи ![]() равносильна выполнимости
условий (28). Соотношения (27) и (28) записаны в
предположении
равносильна выполнимости
условий (28). Соотношения (27) и (28) записаны в
предположении ![]() и
и ![]() . Если в
качестве ограничения принять разрешимость систем неравенств в задачах
. Если в
качестве ограничения принять разрешимость систем неравенств в задачах
![]() и
и ![]() при любых
при любых ![]() и
и
![]() (а это эквивалентно разрешимости систем
(а это эквивалентно разрешимости систем ![]() и
и ![]() ,
, ![]() для всех
для всех
![]() и
и ![]() ), то справедливо утверждение [1,
теорема 3.1]: при выполнимости соотношений
), то справедливо утверждение [1,
теорема 3.1]: при выполнимости соотношений  и
и
 существует непустая область значений параметров r> 0
и R> 0 таких, что
существует непустая область значений параметров r> 0
и R> 0 таких, что
![]()
Так как (25) и (26) находятся в классической двойственности, то opt(25) =opt(26).
В связи с этой теоремой представляет интерес то обстоятельство,
что значения параметров r и R, обеспечивающих
справедливость сформулированной теоремы, обеспечивают ее
справедливость и в ситуации
``урезанных'' совокупностей
функций ![]() и
и ![]() , а именно. Рассмотрим
``урезанные'' задачи
, а именно. Рассмотрим
``урезанные'' задачи
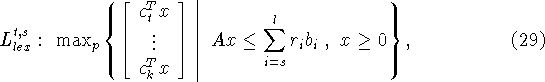
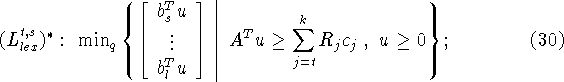
![]() . Для s=0 полагаем
. Для s=0 полагаем ![]() аналогично, если t=0, то полагаем
аналогично, если t=0, то полагаем ![]() . Задачи,
перекрестно скаляризующие (29) и (30), запишутся
в форме:
. Задачи,
перекрестно скаляризующие (29) и (30), запишутся
в форме:
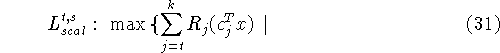
ограничения из (29) },
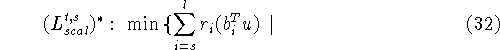
ограничения из (30)}.
Теорема 4.
Пусть системы неравенств ![]() и
и
![]() ,
,
![]() совместны для всех
совместны для всех ![]() и выполнены условия
и выполнены условия 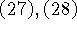 .
Тогда существует непустая область значений параметров r> 0
и
.
Тогда существует непустая область значений параметров r> 0
и ![]() - единых для всех
- единых для всех ![]() и
и ![]() и таких, что
и таких, что
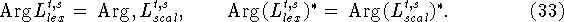
Дадим пояснения к обоснованию сформулированной
теоремы.
Обоснование для случая задач (22), (24) и
(25), (26) в соответствии с работой [2,
теорема 2.1] состоит в последовательном назначении констант:
![]() - для обеспечения эквивалентности (по Arg)
задач (23)
- для обеспечения эквивалентности (по Arg)
задач (23)![]() и
и ![]() , затем
, затем ![]() - для
обеспечения эквивалентности задач (23)
- для
обеспечения эквивалентности задач (23)![]() и
и
![]() и т.д., наконец,
и т.д., наконец, ![]() -
для обеспечения эквивалентности задач (23)
-
для обеспечения эквивалентности задач (23)![]() и
и
![]() .
При этом назначение констант не зависит от r [2,
лемма 2.1]. Значения параметров
.
При этом назначение констант не зависит от r [2,
лемма 2.1]. Значения параметров ![]() , фигурирующих в
формулировке теоремы 4, получаются в силу соотношений
, фигурирующих в
формулировке теоремы 4, получаются в силу соотношений 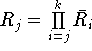 . Так же дело обстоит и с
назначениями параметров
. Так же дело обстоит и с
назначениями параметров ![]() . Из описанной схемы формирования
. Из описанной схемы формирования
![]() и
и ![]() видно, что эти же константы обслуживают
схему эквивалентной сводимости задач (29), (31) к
задачам (30), (32), что и является смыслом
теоремы 4.
видно, что эти же константы обслуживают
схему эквивалентной сводимости задач (29), (31) к
задачам (30), (32), что и является смыслом
теоремы 4.