Соотношения (27), (28), как необходимые условия
разрешимости задач 
и 
при
рассмотрении двойственности, будем считать выполненными. Как
показано, выполнимость их решается процедурой последовательной
оптимальной коррекции.
Вопрос о преодолении несовместности систем ограничений в
(22) и (24) (при всех или некоторых r> 0 и
R> 0) может быть решен в рамках схемы двойственности для
несобственных задач оптимизации. Системы 
и 
разобьем произвольным
образом на подсистемы:
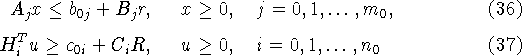
с требованием совместности подсистем
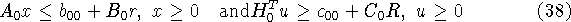
при любых r> 0 и R> 0. Здесь 
-
горизонтальные подматрицы матрицы A, 
- ее
вертикальные подматрицы. Множества их решений обозначим через
и 
соответственно. Условия,
обеспечивающие свойства 
и
, состоят в следующем. Пусть
- столбцы матрицы 
, 
-
столбцы матрицы 
. Первое отмеченное свойство эквивалентно
совместности систем 
второе - совместности систем 
.
По исходным задачам (22) и (24), а также разбиениям
(36) и (37), сконструируем следующие задачи
лексикографической оптимизации:
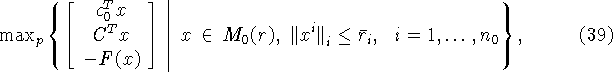
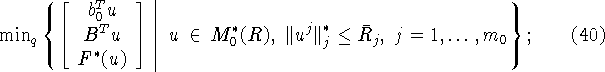
здесь
p и q соответствуют следующим упорядочениям
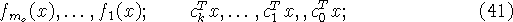
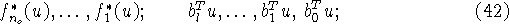
оптимизируемых функций:
и 
- подвекторы
векторов x и u, соответствующие разрезу матрицы
A на вертикальные 
и горизонтальные 
подматрицы ``
'' над 
- сопряженная
норма.
Задачи (39) и (40) синтезируют смысл
последовательной аппроксимации несовместных ограничений задач
(22), (24) и исходной последовательной оптимизации
упорядоченных систем линейных функций 
и
.
Следующий шаг состоит в двойной перекрестной скаляризации этих
задач, а именно:
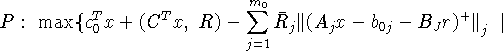
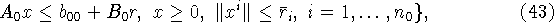
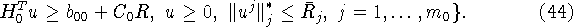
Заметим, что выписанные задачи - это задачи (16) и
(17), в которых выделены критериальные функции 
и
, поставленные в упорядочениях (41) и (42) на
последних местах. Конструкции задач (43) и (44)
являются наиболее общими в исследованиях автора по двойственности для
несобственных задач линейного, паретовского, последовательного и
Парето-последовательного программирования. В задачах (43),
(44) присутствует система векторных и логических параметров,
например, свобода разбиения матрицы A (и параллельно матриц B
и C) на горизонтальные и вертикальные подматрицы, некоторые из
которых могут принимать пустые значения. За счет назначения этих
параметров можно обеспечивать необходимые свойства для
двойственности, аппроксимационного ее смысла и т.д.
Сразу же отметим, что основная нацеленность в изучении задач
(34), (40) и (43), (44) состоит в обеспечении
реализации схемы:
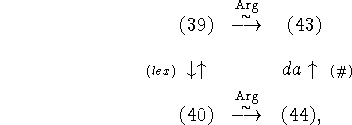
Схема 5.
при этом связь между задачами (43) и (44) обеспечивается свойством регулярной двойственности.
Сформулируем ряд утверждений, подготовляющих доказательство теоремы 5. Для полноты приводится лемма из работы [1, лемма 2.2].
Лемма 1. Для разрешимой задачи
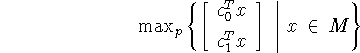
(при р=[1, 0]) выбор числа 
,
обеспечивающего эквивалентный (по Arg) переход к
задаче
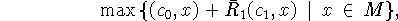
можно осуществить независимо от реализации вектора
b здесь
.
Обобщением ее служит
Лемма 2.
Пусть в разрешимой задаче
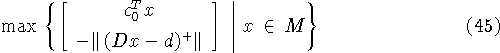
норма кусочно-линейна. Тогда выбор числа
, обеспечивающего эквивалентный (по Arg) переход
от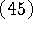 
к задаче
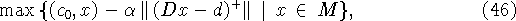
может быть осуществлен независимо от реализации вектора d, при
этом, если для рассматриваемой эквивалентности годится , то
годится и 
.
Доказательство этой леммы
состоит в детализации доказательства леммы 1 с использованием
универсального представления кусочно-линейной нормы
в виде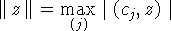 
, при этом 
- размерность пространства переменной
.
Эквивалентный переход от (45) к (46) состоит в применении
метода точных штрафных функций, предполагающий выполнимость условия
регулярности, которое выполняется автоматически для линейных
ситуаций. Внутри постановки (45) содержится задача
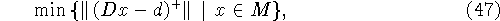
тогда сама задача (45) состоит в
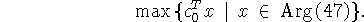
Задачу (47) можно переписать в форме линейной программы
Следовательно, в рассматриваемой ситуации мы не выходим за рамки
линейности, что позволяет без дополнительных предположений применить
технику точных штрафных функций.
Пусть система 
разбита произвольным образом на
подсистемы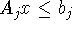 
, 
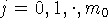, при этом подсистема
- совместна. Выпишем задачи
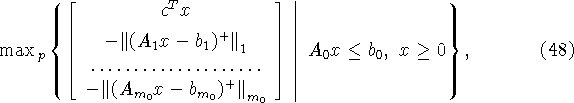
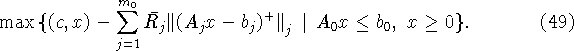
Обобщением леммы 2 служит
Лемма 3.
Если нормы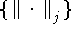 
кусочно-линейны и
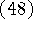разрешима, то выбор параметров 
,
реализующих эквивалентный переход от 
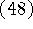к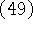 
, может
быть осуществлен независимо от реализации вектора b.
Доказательство проводится путем последовательного применения леммы 2.
З а м е ч а н и е. Обозначения в леммах 1 - 3 мы не связываем прямым образом с обозначениями в задачах (39), (40), (43) и (44), хотя сформулированные леммы подготавливают анализ перечисленных задач.
Выделим некоторые условия, необходимые для формулировки теоремы:
. Выполняются необходимые условия (27), (28)
разрешимости задач (22), (24)
. Все нормы в (43), (44) кусочно-линейны и
монотонны
. Подсистемы 
и
совместны при любых 
и 
.
Теорема 5.
1. Пусть при произвольных R> 0 и r> 0 выполняются
условия 
и 
выбраны в соответствии
.
Тогда задачи Р и 
разрешимы и их оптимальные
значения совпадают.
2. Если выполняются условия - , то существует
непустая область значений параметров R> 0 и r> 0,
, 
таких, что
реализуется схема 5.
Д о к а з а т е л ь с т в о.
1. Сделав в задачах (43), (44)
переобозначения: 
,
,
мы получим формально задачи C и 
из [3, стр. 49], для
которых справедлива теорема 6.12 [3, стр. 60], что эквивалентно
утверждению п. 1 сформулированной выше теоремы 5.1. Что касается
условий упомянутой теоремы 6.12, то они выполняются в силу условий
п. 1 теоремы 5.1.
2. Схема 5 оперирует lex-задачами (39), (40)
и (43), (44), которым присвоены символы P и
. После переобозначений, приведенных в начале п. 1,
последние принимают вид задач P и из [1, стр. 179], а
исходные задачи (39), (40) - вид задач 
,
. Разница между , и
(39), (40) состоит в том, что в последних
lex-оптимизация осуществляется по расширительному списку функций
(41), (42) с расширительным смыслом упорядочений p и
q, соответствующим (41) и (42). Приведенные
сопоставления приводят к редукции п. 2 теоремы 5.1 к
теореме 4.1 [1, стр. 188], в нашем случае выраженной Схемой 5.
Здесь уместно следующее замечание относительно сказанной редукции.
При скаляризации задач (39), (40), т.е. при реализации
переходов (39)
и (40) 
, выбор значений
и 
не зависит от
параметров r и R, в силу чего их выбор, обеспечивающий
упорядочение функций 
и 
в общем
списке упорядочений (41), (42), может осуществляться после
выбора параметров и
. В этом состоит эффект применения лемм 1 и 2.
З а к л ю ч е н и е. Данную работу в определенном
смысле можно считать замыкающей в ряду тех, которые посвящены
симметричной двойственности для некоторых классов задач линейной
оптимизации, а именно, для лексикографической, паретовской и
Парето-лексикографической оптимизации в вариантах их разрешимости
(собственности) и неразрешимости (несобственности). В ней не косвенно
(как в работах [1, 2]), а прямым образом допускается свойство
несобственности для исходных задач. В целом, в работах [1, 2] и
данной определены основные схемы двойственности, сформулированы
теоремы двойственности, затронуты вопросы аппроксимации в случае
неразрешимости задач. Конечно, возможности
обобщений
результатов здесь широкие, в частности, возможности переноса на
случай произвольного пространства и числа критериев произвольной
мощности. Для конечномерной ситуации представляет интерес дальнейшая
разработка введенной автором 
'-оптимизации [2, § 7], связанной
с полиэдральной оптимизацией вообще. Под последней понимаются задачи
оптимизации кусочно-линейных функций при ограничениях в форме систем
кусочно-линейных неравенств без предположений выпуклости, что и
определяет их трудность. Требует нетривиальных усилий и создание
методов, обеспечивающих решение таких задач. Их теоретический анализ
наталкивается на необходимость дальнейшего развития полиэдральной
алгебры.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 96 - 01 - 00116).
Поступила 15.01.96
СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ