при ограничениях
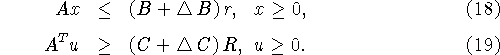
Для приращений
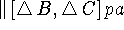 . Если
. Если
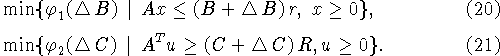
Если
Разрешимость задачи (4) связана, как было сказано, с
совместностью ограничений в задачах (4) и (5). Если эти
условия нарушаются, то коррекцию (или оптимальную коррекцию) можно
осуществить либо за счет коррекции параметров r и R,
либо за счет коррекции матриц B и C. Рассмотрим
конструкцию оптимальной коррекции (аппроксимации) матриц B и
C для обеспечения совместности систем ограничений в
задачах (4), (5), т.е. разрешимости этих задач. Пусть
![]() и
и ![]() - приращения для матриц B и
C, рассматриваемых как векторы пространств R
- приращения для матриц B и
C, рассматриваемых как векторы пространств R![]() и
R
и
R![]() соответственно, т.е.
соответственно, т.е. ![]() R
R![]() ,
, ![]() R
R![]() . Если ввести функцию ``качества''
этих приращений
. Если ввести функцию ``качества''
этих приращений ![]() , то можно поставить
задачу коррекции в форме: найти
, то можно поставить
задачу коррекции в форме: найти
![]()
при ограничениях
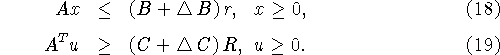
Для приращений ![]() и
и ![]() можно ввести допустимые
области, чего мы делать не будем во избежание громоздкости. Функция
можно ввести допустимые
области, чего мы делать не будем во избежание громоздкости. Функция
![]() может быть нормой
может быть нормой 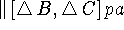 . Если
. Если
![]() ,
то сформулированная задача коррекции распадется на две независимые
задачи:
,
то сформулированная задача коррекции распадется на две независимые
задачи:
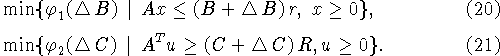
Если ![]() и
и ![]() - линейные функции, т.е.
- линейные функции, т.е.
![]() ,
, ![]() , где
, где
![]() и
и ![]() - фиксированные
векторы из пространств приращений
- фиксированные
векторы из пространств приращений ![]() и
и ![]() , то
задачи (20) и (21) - задачи ЛП. Найдя из них
оптимальные
, то
задачи (20) и (21) - задачи ЛП. Найдя из них
оптимальные ![]() и
и ![]() и подставив в
(18), (19), получим совместные относительно x и u
системы неравенств, что обеспечивает разрешимость задач (4) и
(5) при замене B и C на
и подставив в
(18), (19), получим совместные относительно x и u
системы неравенств, что обеспечивает разрешимость задач (4) и
(5) при замене B и C на ![]() и
и ![]() . В случае
. В случае ![]() ,
, ![]() задачи (20) и (21) суть задачи квадратичного
программирования, для которых (как и для задач ЛП) существуют
эффективные методы их решения.
задачи (20) и (21) суть задачи квадратичного
программирования, для которых (как и для задач ЛП) существуют
эффективные методы их решения.