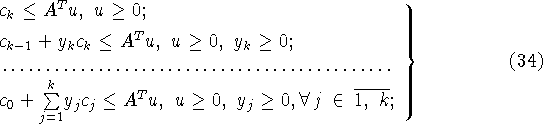
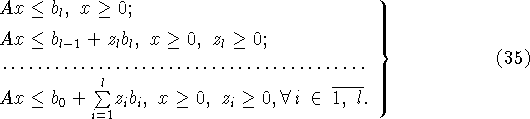
Нарушение того или иного включения из (27), (28) выражается в несовместности соответствующей системы линейных неравенств из (34), (35). Коррекция задач
Неразрешимость задачи (22) состоит либо в несовместности
системы ее ограничений (при заданном r), либо в невыполнимости
одного из включений (27). Так же дело обстоит и с неразрешимостью
задачи (24): либо ее система ограничений несовместна (при
заданном k), либо не выполняется одно из включений (28).
Включения (27) и (28) могут быть эквивалентно записаны
в форме последовательностей систем линейных неравенств:
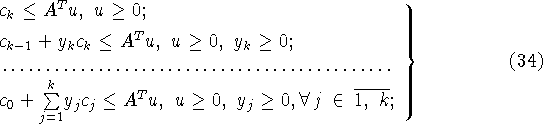
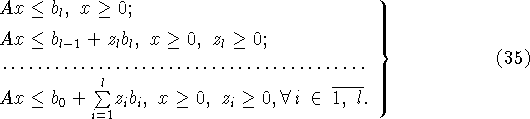
Нарушение того или иного включения из (27), (28)
выражается в несовместности соответствующей системы линейных
неравенств из (34), (35). Коррекция задач ![]() и
и
![]() , т.е. (22) и (24), может быть
осуществлена за счет коррекции векторов
, т.е. (22) и (24), может быть
осуществлена за счет коррекции векторов ![]() и
и
![]() по следующей схеме.
по следующей схеме.
Рассмотрим первую систему из (34), т.е. ![]() . Нарушение первого включения из (27) означает
несовместность последней. Вектором невязки для нее будет
. Нарушение первого включения из (27) означает
несовместность последней. Вектором невязки для нее будет ![]() , где ``+'' над вектором означает замену его отрицательных
координат нулями (положительная срезка). Если в силу некоторой нормы
, где ``+'' над вектором означает замену его отрицательных
координат нулями (положительная срезка). Если в силу некоторой нормы
![]() определить уклонение
определить уклонение ![]() и
и ![]() , то вектор
, то вектор ![]() будет минимальной (по критерию введенной нормы
будет минимальной (по критерию введенной нормы ![]() )
коррекцией вектора
)
коррекцией вектора ![]() , обеспечивающей совместность системы
, обеспечивающей совместность системы ![]() , или (что одно и то же) выполнение
включения
, или (что одно и то же) выполнение
включения ![]() cone
cone![]() при
при ![]() . Подставив во вторую систему из (34)
. Подставив во вторую систему из (34) ![]() вместо
вместо ![]() , аналогично подсчитаем
, аналогично подсчитаем ![]() путем
введения для вектора-невязки своей нормы
путем
введения для вектора-невязки своей нормы ![]() и
т.д.
и
т.д.
Если в качестве вводимых выше норм брать монотонные кусочно-линейные нормы, то все задачи коррекции преобразуются в задачи линейного программирования.
Сделаем еще одно замечание: выполнимость соотношений (27),
(28) эквивалентна тому, что ![]() в приведенной схеме
оптимальной коррекции.
в приведенной схеме
оптимальной коррекции.