5. Свойства множеств достижимости динамических систем с разрывными траекториями

Здесь будут обсуждаться свойства множества $V$-решений нелинейной системы дифференциальных уравнений с обобщенным воздействием - импульсным управлением, подчиненным интегральному ограничению. Материал этого раздела включает результаты, опубликованные в [32,33,34,54].

Согласно теореме 1, каждая пара функций $(v(t),V(t))$ порождает некоторое множество $V$-решений уравнения (1.1). Обозначим через $V(\cdot\vert a)$ множество $(m+1)$-мерных абсолютно непрерывных вектор-функций, первые $m$ координат которых - вектор-функции $v(t)$, а $(m+1)$-я координата - $\mathop{\rm var}\limits_{[{t_0},\,{t}]} v(\cdot)$, причем для всех $v(t)$ выполняется неравенство $\mathop{\rm var}\limits_{[{t_0},\,{t}]} v(\cdot) \leq a$.

Пару функций ограниченной вариации $v(t)$ со значениями в $R^m$ и $V(t)$ со значениями в $R^1$ будем называть совместимой, если для любых $t_1$ и $t_2$, удовлетворяющих условию $t_0 \leq t_1 <t_2 \leq \vartheta$, выполняется неравенство

$$V(t_1) + \mathop{\rm var}\limits_{[{t_1},\,{t_2}]} v(\cdot) ... ... a - \mathop{\rm var}\limits_{[{t_2},\,{\vartheta}]} v(\cdot).$$ (5.1)

Из (5.1), в частности, следует, что $\mathop{\rm var}\limits_{[{t_0},\,{\vartheta}]} v(\cdot) \leq a,$ а также $V(\vartheta) \leq a$. Совместимые пары $(v(t),\,V(t))$ далее будем обозначать через $w(t)=(v(t),\,V(t))$, а все множество совместимых пар $w(t)$ - через $W(\cdot\vert a)$.

Доказано, что множество $W(\cdot\vert a)$ является замыканием множества
$V(\cdot\vert a)$ в топологии поточечной сходимости.

Обозначим через $X(t,w(\cdot))$ множество всех $V$-решений системы дифференциальных уравнений (1.1), порожденных совместимой парой функций $w(t)=(v(t),\,V(t))$ и удовлетворяющих начальному условию $x(t_{0}) =x^{0}.$ Доказана следующая

Теорема 7.   Множество $X(t,w(\cdot))$ компактно в топологии поточечной сходимости.

Обозначим через $\lim_{k \to \infty}X(t,w_k(\cdot))$ множество поточечных частичных пределов произвольных последовательностей $x_k(t)$, где $x_k(t) \in X(t,w_k(\cdot))$.

Теорема 8.   Пусть для каждого $t\in [t_o,\,\vartheta]$ последовательность функций ограниченной вариации $w_k(t)$ поточечно сходится к $w(t)$. Тогда справедливо включение

$$\lim_{k\to\infty} X(t,w_k(\cdot))\subset X(t,w(\cdot)).$$

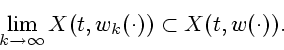
З а м е ч а н и е. Обратное включение, вообще говоря, верным не является.

Обозначим через $X_W(t,a)$ объединение множеств $X(t,w(\cdot))$ по всем допустимым $w(\cdot) \in W(\cdot\vert a)$.

Теорема 9.   Множество $X_W(t,a)$ компактно в топологии поточечной сходимости.

Обозначим через $X_V(t,a)$ множество решений системы дифференциальных уравнений (5.1), порожденных абсолютно непрерывными управлениями $v(t),\,V(t)=\mathop{\rm var}\limits_{[{t_0},\,{t}]}v(\cdot)$, подчиненными ограничению $\mathop{\rm var}\limits_{[{t_0},\,{t}]} v(\cdot) \leq a$, т.е. управлениями из класса $V(\cdot\vert a)$, а через $X_{\check V}(t,a)$ - множество $V$-решений системы (5.1), порожденных функциями ограниченной вариации $v(t),$
$V(t)=\mathop{\rm var}\limits_{[{t_0},\,{t}]}v(\cdot),$ подчиненными ограничению $\mathop{\rm var}\limits_{[{t_0},\,{t}]} v(\cdot) \leq a$, т.е. порожденных функциями из класса $\check V(\cdot\vert a)$.

Очевидно включение

$$X_V(t,a) \subset X_{\check V}(t,a) \subset X_W(t,a).$$ (5.2)

Теорема 10.   $\bar X_V(t,a) = \bar X_{\check V}(t,a) = X_W(t,a).$

Предположим, что правая часть системы дифференциальных уравнений (1.1) зависит от параметра $\lambda,$ т.е. уравнение (1.1) имеет вид

$$\dot x=f(t,x,v,V,\lambda)+ B(t,x,v,V,\lambda) \dot v(t).$$ (5.3)

Множества $X(t,w(\cdot))$ и $X_W(t,a)$ в данном случае будем обозначать соответственно через $X(t,w(\cdot),\lambda)$ и $X_W(t,a,\lambda).$

Множествам $X_W(t,a)$ и $X_W(t,a,\lambda)$ можно поставить в соответствие многозначные отображения $X^*_W(t,a)$ и $X^*_W(t,a,\lambda),$ отображающие отрезок $[t_0,\vartheta]$ в $R^n$ по следующему правилу: $x \in X^*_W(t,a)$ $(x\in X^*_W(t,a,\lambda)),$ если существует такая пара $w(t)\in W(\cdot\vert a),$ что среди порожденных ею траекторий системы (1.1) (или (5.3)) существует такая траектория $x(t),$ что $x=x(t).$ Аналогичным образом можно определить многозначные отображения $X^*(t,w(\cdot))$ и $X^*(t,w(\cdot),\lambda).$

Через $\rho (Y,Z)$ обозначим хаусдорфово расстояние между компактными множествами $Y$ и $Z$,

$$\rho (Y,Z) = \max \left\{ \max_{y \in Y} \min_{z\in Z} \vert y-z\vert, \max_{z\in Z} \min_{y\in Y} \vert y-z\vert \right\}.$$

Определение 3.   Будем говорить, что множество $X^*_W(t,a,\lambda)$ непрерывно зависит от параметра $\lambda$ при $\lambda =\lambda_0,$ если для каждого $t \in [t_0, \vartheta]$ выполняется условие

$$\lim_{\lambda \to \lambda_0} \rho (X^*_W(t,a,\lambda), X^*_W(t,a,\lambda_0)) = 0.$$

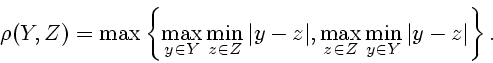
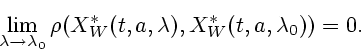
Аналогичным образом можно дать определение непрерывной зависимости от параметра $\lambda$ множества $X^*(t,w(\cdot),\lambda)$ и определение непрерывной зависимости множества $X^*_W(t,a,\lambda)$ от ресурса управления $a.$

Теорема 11.   Пусть правая часть уравнения $(\ref{8.1})$ удовлетворяет условиям теоремы $1$. Кроме того, предположим, что для всех допустимых $t,\,x,\,v,\,V$ и для произвольного $\varepsilon > 0$ найдется такое $\delta = \delta (\varepsilon)>0,$ что для всех $\lambda,$ $\vert\lambda - \lambda_0 \vert<\delta,$ выполняются неравенства

$$\vert f(t,x,v,V,\lambda) - f(t,x,v,V,\lambda_0)\vert < \varepsilon,$$

$$\Vert B(t,x,v,V,\lambda) - B(t,x,v,V,\lambda_0)\Vert < \varepsilon.$$

Тогда для всех $t \in [t_0, \vartheta]$ множество $X^*_W(t,a,\lambda)$ непрерывно зависит от параметра $\lambda$ в точке $\lambda = \lambda_0.$

Заметим, что при предположениях теоремы 11 можно доказать аналогичный результат и для множества $X^*(t,w(\cdot),\lambda).$

Теперь предположим, что объект управления описывается системой дифференциальных уравнений (1.1). Обозначим через $P \in R^n$ ограниченное замкнутое множество, содержащее в себе $X_W(t,a),$ а через $Q$ - шар радиуса $a$ в $R^m$ с центром в начале координат. Очевидно, что $v(t) \in Q$ для всех $t\in [t_0,\vartheta].$

Теорема 12.   Пусть $f(t,x,v,V)$ и $B(t,x,v,V)$ удовлетворяют условиям теоремы $1$ и непрерывны по совокупности переменных $(t,x,v,V)$ в области $[t_0,\vartheta]\times P \times Q \times [0,a].$ Тогда $X^*_W(t,a)$ непрерывно зависит от величины ресурса управления $a.$

Будем рассматривать множество достижимости $X^*_W(t,a)$ как многозначное отображение [3]. Это отображение порождается, вообще говоря, разрывными функциями ограниченной вариации. Тем не менее оказывается, что многозначное отображение $X^*_W(t,a)$ разрывно лишь в точке $t=t_0.$

Теорема 13.   Многозначное отображение $X^*_W(t,a)$ непрерывно на множестве $(t_0,\vartheta].$

Теперь рассмотрим вопрос о связности множества достижимости. Сначала напомним два определения.

Множество $A$ называется связным, если его нельзя представить в виде объединения двух непустых открытых в $A$ подмножеств [36].

Множество $A$ называется линейно связным, если для любых точек $x_0,\,\,x_1 \in A$ существует такая непрерывная функция $q:$ $[0,1] \to A,$ что $q(0)=x_0,\,\, q(1)=x_1$ [36].

Очевидно, что всякое линейно связное множество является связным.

Лемма 2.   Пусть система $(\ref{1.1})$ удовлетворяет условиям теоремы $1$ и матрица-функция $B(t,x,v,V)$ удовлетворяет условию Липшица по переменной $v.$ Тогда множество $X(t,w(\cdot))$ линейно связно.

Теорема 14.   При предположениях леммы $2$ множество $X_W(t,a)$ является связным.

Поступила 18.10.99