

Next: 4 Аппроксимируемые решения нелинейных
Up: SESEKIN
Previous: 2 Определение разрывного решения
Пусть
- начальные условия для
системы
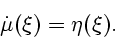 |
(3.1) |
Обозначим через
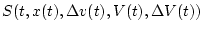 (где
(где 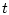 может принимать значения
может принимать значения 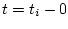 или
или 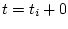 ) множество,
получающееся сдвигом на величину
) множество,
получающееся сдвигом на величину 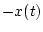 в момент
в момент 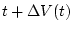 сечения множества достижимости системы (3.1).
Предполагается, что в (3.1)
сечения множества достижимости системы (3.1).
Предполагается, что в (3.1)
где управление 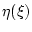 подчинено ограничению
подчинено ограничению
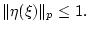
Эта теорема была опубликована в [31]. Из других
результатов, посвященных описанию разрывных решений (в случае,
если реакция системы на импульсное управление определяется не
единственным образом) следует отметить работы
[23,29,40,48].
Следующая теорема [33] дает простое условие,
обеспечивающее единственность 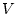 -решения.
-решения.
Теорема 2.
Пусть
![$V(t)=\mathop{\rm var}\limits_{[{t_{0}},\,{t}]} v(\cdot).$](img107.gif) Тогда интегральное
включение
Тогда интегральное
включение 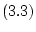 превращается в интегральное уравнение
и пара
превращается в интегральное уравнение
и пара 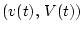 порождает единственное
порождает единственное 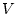 -решение
уравнения
-решение
уравнения 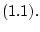
Близкий результат с использованием другой техники получен в
[41].
Примеры.
Рассмотрим следующую задачу Коши:
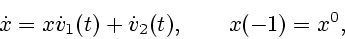 |
(3.4) |
где
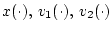 - скалярные
функции. Пусть
- скалярные
функции. Пусть
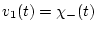 ,
,
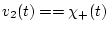 (функции
(функции 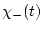 и
и 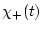 определяются формулами (1.5) и (1.7)) и
определяются формулами (1.5) и (1.7)) и
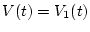 , где
, где
Согласно теореме 2 (
![$V_{1}(t)=\mathop{\rm var}\limits_{[{t_{0}},\,{t}]}
v(\cdot),\, v(t)=(v_{1}(t),\,v_{2}(t))^{T})$](img118.gif) ,
, 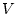 -решение
задачи
Коши (3.4) будет иметь вид
-решение
задачи
Коши (3.4) будет иметь вид
Если
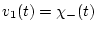 ,
,
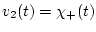 , а
, а
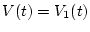 , то
, то 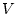 -решение определяется формулой
-решение определяется формулой
Пусть
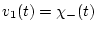 ,
,
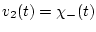 и
и
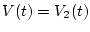 , где
, где
В этом случае вновь
![$V_{2}(t)=\mathop{\rm var}\limits_{[{t_{0}},\,{t}]} v(\cdot)$](img125.gif) и
согласно теореме 2
и
согласно теореме 2 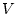 -решение уравнения
(3.4) представимо в виде
-решение уравнения
(3.4) представимо в виде
Пусть
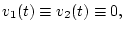 а
а
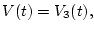 где
где
Проаппроксимируем функцию 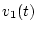 последовательностью
последовательностью
а функцию 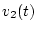 - последовательностью
- последовательностью
Очевидно, что
![$\mathop{\rm var}\limits_{[{t_0},\,{t}]}v_{k\,i}(\cdot)\to V_3(t),$](img134.gif)
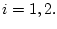 Нетрудно вычислить, что последовательность
Нетрудно вычислить, что последовательность 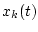 решений
уравнения (3.4), порожденная предложенными аппроксимациями
функций
решений
уравнения (3.4), порожденная предложенными аппроксимациями
функций 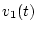 и
и 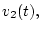 будет сходиться к функции
будет сходиться к функции
Если положить
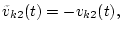 то последовательность
то последовательность
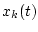 будет сходиться к
будет сходиться к
Далее будет отмечено, что все множество 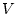 -решений, порожденное
парой
-решений, порожденное
парой 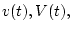 связно. Следовательно, кроме полученных двух
связно. Следовательно, кроме полученных двух
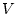 -решений уравнения (3.4) и всякая функция
-решений уравнения (3.4) и всякая функция
где
![$c\in[-\frac{1}{2}(\exp{(-1/2)}-1),\,\frac{1}{2}(\exp{(-1/2)}-1)],$](img143.gif) также будет
также будет 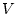 -решением уравнения (3.4). Таким образом,
интегральная воронка решений, порожденная парой непрерывных
функций
-решением уравнения (3.4). Таким образом,
интегральная воронка решений, порожденная парой непрерывных
функций
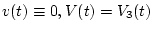 содержит одну непрерывную
траекторию
содержит одну непрерывную
траекторию
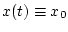 и континуум разрывных траекторий.
и континуум разрывных траекторий.
Рассмотрим математическую модель вертикального подъема ракеты
[15], оснащенной двумя двигателями с различными удельными
импульсами (импульсами, приходящимися на единицу массы
израсходованного топлива):
![\begin{displaymath}
\begin{array}{rcl}
\dot x_1\!\!\! & = & \!\!\!x_2,\\ [2ex] \...
...!\displaystyle - \frac{P_1}{C_1} - \frac{P_2}{C_2},
\end{array}\end{displaymath}](img146.gif) |
(3.5) |
где 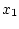 - высота полета,
- высота полета, 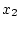 - скорость полета,
- скорость полета, 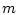 - масса
ракеты,
- масса
ракеты, 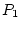 и
и 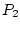 - реактивные управляющие силы, допускающие
дискретный расход топлива. Согласно теореме 1, реакция
системы (3.5) на импульсное воздействие, вообще говоря,
неединственна. Предположим, что реактивные силы в (3.5) не
могут менять своего направления. Это предположение накладывает
геометрическое ограничение вида
- реактивные управляющие силы, допускающие
дискретный расход топлива. Согласно теореме 1, реакция
системы (3.5) на импульсное воздействие, вообще говоря,
неединственна. Предположим, что реактивные силы в (3.5) не
могут менять своего направления. Это предположение накладывает
геометрическое ограничение вида
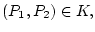 где
где 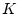 -
замкнутый выпуклый конус с вершиной в нуле (например
-
замкнутый выпуклый конус с вершиной в нуле (например 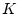 - первый
квадрант на плоскости
- первый
квадрант на плоскости 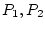 ), на аппроксимации обобщенного
управления. Такие ограничения рассматривались, например, в
[23]. Заметим, что теоремы 1 и 2
остаются верными и при таких геометрических ограничения с той лишь
поправкой, что при построении множества
), на аппроксимации обобщенного
управления. Такие ограничения рассматривались, например, в
[23]. Заметим, что теоремы 1 и 2
остаются верными и при таких геометрических ограничения с той лишь
поправкой, что при построении множества
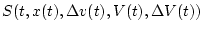 в качестве допустимого множества для
управления
в качестве допустимого множества для
управления 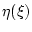 системы (3.1) будет рассматриваться
шар
системы (3.1) будет рассматриваться
шар
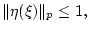 пересеченный с конусом
пересеченный с конусом 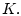 В
рассматриваемом примере функции
В
рассматриваемом примере функции 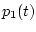 и
и 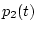 -
первообразные от
-
первообразные от 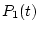 и
и 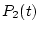 будут монотонными, а для
монотонных функций
будут монотонными, а для
монотонных функций
![\begin{displaymath}\mathop{\rm var}\limits_{[{t_0},\,{t}]} p_i(\cdot) = p_i(t) - p_i(t_0)
\qquad (i=1,2).\end{displaymath}](img160.gif)
Поэтому из поточечной сходимости
аппроксимирующих последовательностей к первообразным от
управляющих функций будет следовать и сходимость соответствующих
последовательностей из вариаций этих функций к вариациям
предельных функций. Таким образом, в данном случае будут
выполняться условия теоремы 2 и, следовательно, для
каждого начального условия система (3.5) будет иметь
единственное 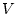 -решение.
-решение.
Пусть управляющие силы действуют на объект управления в момент
времени 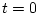 импульсами интенсивности
импульсами интенсивности 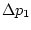 и
и 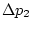 соответственно. Вычислим согласно формулам (3.1) величины
скачков скорости
соответственно. Вычислим согласно формулам (3.1) величины
скачков скорости 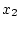 и массы
и массы 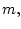 произошедших в результате
действия импульсов. Получим
произошедших в результате
действия импульсов. Получим
С учетом первого равенства, второе можно записать в
виде
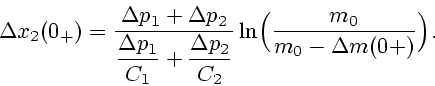 |
(3.6) |
Заметим, что (3.6) обобщает формулу Циолковского [18]
на случай ракеты с двумя двигателями с различными удельными
импульсами. Обычную формулу Циолковского можно получить из
(3.6), полагая в ней
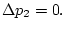
Если отказаться от предположения о том, что управляющие
воздействия не меняют направления своего действия, то реакция
системы (3.5) на импульсное управление может оказаться
неоднозначной.


Next: 4 Аппроксимируемые решения нелинейных
Up: SESEKIN
Previous: 2 Определение разрывного решения
2003-06-03
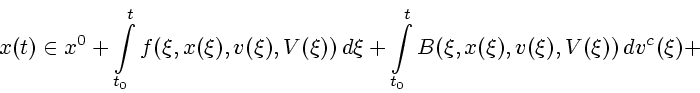
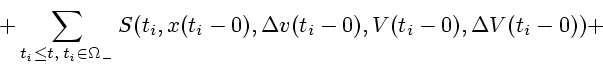
![]() включения
включения ![]() порожденного парой функций
порожденного парой функций ![]() , существует
последовательность абсолютно непрерывных функций
, существует
последовательность абсолютно непрерывных функций ![]() ,
поточечно сходящаяся к
,
поточечно сходящаяся к ![]() и удовлетворяющая условию
и удовлетворяющая условию
![]() такая, что соответствующая последовательность
такая, что соответствующая последовательность
![]() решений уравнения
решений уравнения ![]() будет поточечно
сходиться к
будет поточечно
сходиться к ![]() .
.![]() -решения.
-решения.
![\begin{displaymath}V_{1}(t)= \left\{ \begin{array}{ll}
0, & \mbox{$t<0$}, \\ [2...
...\mbox{$t=0$}, \\ [2mm]
2, & \mbox{$t>0$}.
\end{array} \right.\end{displaymath}](img117.gif)
![]() ,
,
![]() , а
, а
![]() , то
, то ![]() -решение определяется формулой
-решение определяется формулой
![]() ,
,
![]() и
и
![]() , где
, где
![\begin{displaymath}V_{2}(t)= \left\{ \begin{array}{ll}
0, & \mbox{$t<0$}, \\ [2mm]
\sqrt{2}, & \mbox{$t\geq 0$}.
\end{array} \right.\end{displaymath}](img124.gif)
![]() а
а
![]() где
где
![\begin{displaymath}V_{3}(t)= \left\{
\begin{array}{ll}
0, & \mbox{$t<0$}, \\ [2mm]
2, & \mbox{$t \leq 0$}.
\end{array} \right.\end{displaymath}](img129.gif)
![\begin{displaymath}v_{k1}(t)= \left\{
\begin{array}{rl}
0, & \quad t\not\in [-4...
... -\frac{1}{2} k, &\quad t \in [-2/k,-1/k],
\end{array} \right.\end{displaymath}](img131.gif)
![\begin{displaymath}v_{k2}(t)= \left\{
\begin{array}{rl}
0, & \quad t\not\in [-3...
...x]
-\frac{1}{2} k, &\quad t \in [-1/k,0].
\end{array} \right.\end{displaymath}](img133.gif)
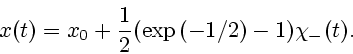
![]() то последовательность
то последовательность
![]() будет сходиться к
будет сходиться к
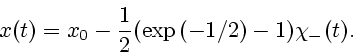
![]() -решений, порожденное
парой
-решений, порожденное
парой ![]() связно. Следовательно, кроме полученных двух
связно. Следовательно, кроме полученных двух
![]() -решений уравнения (3.4) и всякая функция
-решений уравнения (3.4) и всякая функция
![\begin{displaymath}\mathop{\rm var}\limits_{[{t_0},\,{t}]} p_i(\cdot) = p_i(t) - p_i(t_0)
\qquad (i=1,2).\end{displaymath}](img160.gif)
![]() импульсами интенсивности
импульсами интенсивности ![]() и
и ![]() соответственно. Вычислим согласно формулам (3.1) величины
скачков скорости
соответственно. Вычислим согласно формулам (3.1) величины
скачков скорости ![]() и массы
и массы ![]() произошедших в результате
действия импульсов. Получим
произошедших в результате
действия импульсов. Получим
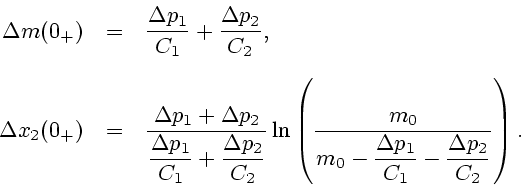
![]()