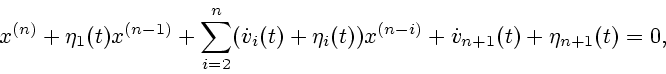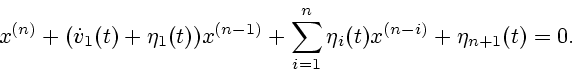

Next: 5 Свойства множеств достижимости
Up: SESEKIN
Previous: 3 -решения нелинейных систем
Здесь мы рассмотрим классы нелинейных дифференциальных
уравнений, для которых предельная траектория не зависит от
способа аппроксимации обобщенного воздействия.
Рассмотрим следующую задачу Коши:
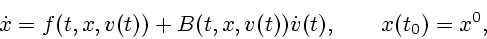 |
(4.1) |
Заметим, что правая часть уравнения в (4.1), в отличие от
(1.1), не зависит от 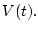
С помощью этой леммы доказана следующая
Теорема 3.
Пусть в области
![$t \in [t_{0},\vartheta],\, x \in R^{n},\,
\Vert v\Vert _{p} \leq M$](img169.gif) элементы матрицы
элементы матрицы 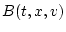 удовлетворяют
условиям леммы
удовлетворяют
условиям леммы  вектор-функция
вектор-функция 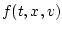 непрерывна по
совокупности переменных, липшицева по
непрерывна по
совокупности переменных, липшицева по 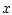 и удовлетворяет
неравенству
Тогда для
всякой вектор-функции
и удовлетворяет
неравенству
Тогда для
всякой вектор-функции
![$v(t) \in BV_{n}[t_{0},\vartheta]$](img187.gif) существует аппроксимируемое решение
существует аппроксимируемое решение 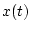 задачи Коши
задачи Коши
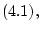 которое удовлетворяет интегральному уравнению
где
которое удовлетворяет интегральному уравнению
где
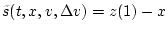 ,
,
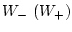 -
множество точек левого (правого) разрывов вектор-функции
-
множество точек левого (правого) разрывов вектор-функции
Близкий результат был сформулирован в [22], а полное
доказательство впервые опубликовано в работе [27].
Следует отметить также работы [25,37,38,39].
Последующие результаты этого раздела опубликованы в
[14,30,54]. Предположим, что система (4.1) имеет
вид
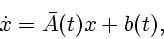 |
(4.2) |
где
- 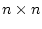 -матрица с непрерывными элементами,
-матрица с непрерывными элементами, 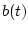 - вектор с суммируемыми элементами,
- вектор с суммируемыми элементами,
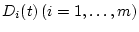 -
непрерывные
-
непрерывные 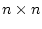 -матрицы-функции,
-матрицы-функции, 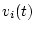 - компоненты
вектора
- компоненты
вектора
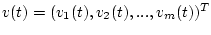 - функции
ограниченной вариации. Для системы обычных дифференциальных
уравнений (4.2) справедлива
- функции
ограниченной вариации. Для системы обычных дифференциальных
уравнений (4.2) справедлива
Теорема 4.
Пусть матрицы
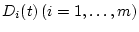 для каждого
для каждого
![$t\in[t_{0},\vartheta]$](img71.gif) взаимно коммутативны. Тогда всякое
аппроксимируемое решение однородной системы
взаимно коммутативны. Тогда всякое
аппроксимируемое решение однородной системы
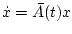 с начальным условием
с начальным условием
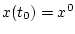 представимо в виде
представимо в виде
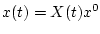 , где
, где 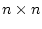 -матрица
-матрица 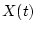 -
аппроксимируемое решение матричного уравнения
-
аппроксимируемое решение матричного уравнения
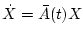 с начальным условием
с начальным условием 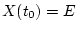 , которое удовлетворяет
уравнению
где
Для
аппроксимируемого решения уравнения
, которое удовлетворяет
уравнению
где
Для
аппроксимируемого решения уравнения 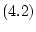 справедлива
формула Коши
справедлива
формула Коши
Далее будем полагать матрицы 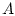 и
и
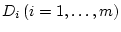 постоянными. Теперь система (4.2) примет вид
постоянными. Теперь система (4.2) примет вид
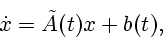 |
(4.3) |
где
Теорема 5.
Пусть матрицы
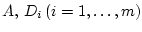 взаимно коммутативны.
Тогда аппроксимируемое решение уравнения
взаимно коммутативны.
Тогда аппроксимируемое решение уравнения 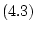 представимо в виде
где
представимо в виде
где
Рассмотрим нелинейное дифференциальное уравнение 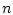 -го
порядка
-го
порядка
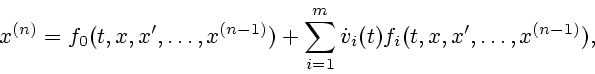 |
(4.4) |
где 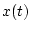 - скалярная функция;
- скалярная функция;
непрерывны по 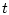 и липшицевы по
и липшицевы по
 на множестве
на множестве
![$t\in [t_{0},\vartheta],$](img227.gif)
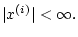
Аналогично определению 1 можно ввести понятие аппроксимируемого
решения для уравнения (4.4) и показать, что если
уравнение (4.4) представимо в виде
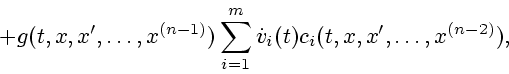 |
(4.5) |
то существует аппроксимируемое решение уравнения (4.4).
Пусть линейное дифференциальное уравнение имеет вид
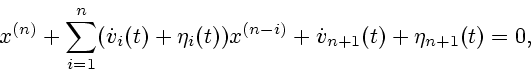 |
(4.6) |
где
![$v_{i}(t) \in BV[t_{0},\vartheta], \, \eta_i (t)$](img232.gif) -
непрерывные на
-
непрерывные на
![$[t_{0},\vartheta]$](img20.gif) функции,
функции,
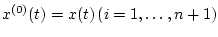 .
.
Теорема 6.
Аппроксимируемое решение уравнения 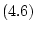 существует
тогда и только тогда, когда уравнение
существует
тогда и только тогда, когда уравнение 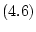 имеет вид
либо
имеет вид
либо


Next: 5 Свойства множеств достижимости
Up: SESEKIN
Previous: 3 -решения нелинейных систем
2003-06-03
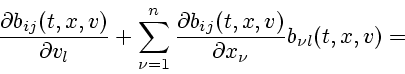
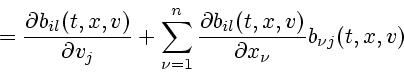
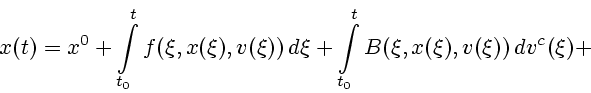
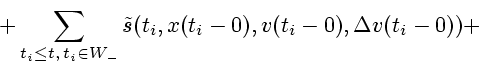
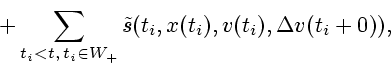
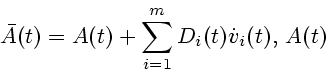
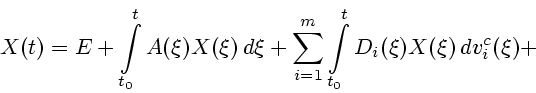
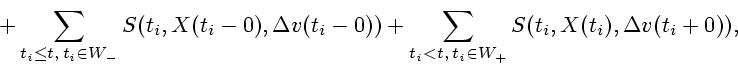
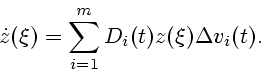
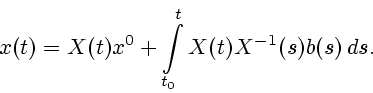
![]() и
и
![]() постоянными. Теперь система (4.2) примет вид
постоянными. Теперь система (4.2) примет вид
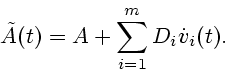
![\begin{displaymath}x(t) = \exp{[\tilde A^{*}(t)-\tilde
A^{*}(t_{0})]}
x^{0}+\in...
...s_{t_{0}}^{t}
\exp{[\tilde A^{*}(t)-\tilde A^{*}(s)]} b(s)\,ds,\end{displaymath}](img221.gif)
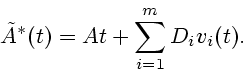
![]() -го
порядка
-го
порядка