| (1.1) |
Рассмотрим следующую задачу Коши:
Здесь ![]() ,
, ![]() - соответственно
- соответственно ![]() и
и ![]() -мерные
вектор-функции времени,
-мерные
вектор-функции времени,
![]() -
- ![]() -мерная
вектор-функция и
-мерная
вектор-функция и
![]() -
- ![]() -матрица-функция,
-матрица-функция,
![]() ,
,
![]()
![]() -
банахово пространство
-
банахово пространство ![]() -мерных функций ограниченной вариации.
Предположим, что
-мерных функций ограниченной вариации.
Предположим, что
![]() и
и
![]() непрерывны по совокупности переменных
и липшицевы по
непрерывны по совокупности переменных
и липшицевы по ![]() на множестве
на множестве
![]() где
где
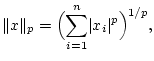 и удовлетворяют следующим стандартным условиям на том же
множестве:
и удовлетворяют следующим стандартным условиям на том же
множестве:
Если ![]() - абсолютно непрерывная вектор-функция,
определенная на отрезке
- абсолютно непрерывная вектор-функция,
определенная на отрезке
![]() , то в рамках
теоремы Каратеодори [35] решение задачи Коши (1.1)
существует, единственно и удовлетворяет интегральному уравнению
, то в рамках
теоремы Каратеодори [35] решение задачи Коши (1.1)
существует, единственно и удовлетворяет интегральному уравнению
Если функцию ![]() считать функцией ограниченной вариации, то
один из подходов к обсуждаемой проблеме состоит в замене
дифференциального уравнения в (1.1) интегральным
(1.2), в котором интеграл понимается в смысле
Лебега-Стилтьеса или Перрона-Стилтьеса
[2,42,49,51,52,53].
считать функцией ограниченной вариации, то
один из подходов к обсуждаемой проблеме состоит в замене
дифференциального уравнения в (1.1) интегральным
(1.2), в котором интеграл понимается в смысле
Лебега-Стилтьеса или Перрона-Стилтьеса
[2,42,49,51,52,53].
Необходимость отказаться от интеграла Римана-Стилтьеса
вызвана следующим обстоятельством. Если
![]() , то естественно ожидать, что
, то естественно ожидать, что ![]() будет принадлежать
будет принадлежать
![]() Тогда точки
разрыва функции
Тогда точки
разрыва функции ![]() будут точками разрыва функции
будут точками разрыва функции ![]() и
интеграл Римана-Стилтьеса существовать не будет.
и
интеграл Римана-Стилтьеса существовать не будет.
Но если интеграл в (1.2) понимать в смысле
Лебега-Стилтьеса или Перрона-Стилтьеса, то,
очевидно, величины скачков решения будут зависеть от
определения интегрируемой функции в точках разрыва функции
![]() Это обусловлено тем, например, что мера
Лебега-Стилтьеса точки не обязательно равна нулю.
Это обусловлено тем, например, что мера
Лебега-Стилтьеса точки не обязательно равна нулю.
Проиллюстрируем этот подход к определению решения задачи Коши
(1.1) на примере
Если
![]() , где
, где ![]() - функция
Хевисайда, непрерывная справа (разрывная слева) в точке
- функция
Хевисайда, непрерывная справа (разрывная слева) в точке ![]() :
:
Далее, в случае, когда конечный результат не зависит от того,
слева или справа непрерывна единичная функция Хевисайда, мы будем
обозначать ее через ![]() Заметим, что при
Заметим, что при
![]() уравнение (1.4) в случае
уравнение (1.4) в случае ![]() решения не имеет, а величина
скачка в момент
решения не имеет, а величина
скачка в момент ![]() стремится к бесконечности при
стремится к бесконечности при ![]() . Этот
подход развивался в работах [2,42,49,51,52,53].
. Этот
подход развивался в работах [2,42,49,51,52,53].
Следующий подход состоит в формализации настоящей задачи в
рамках теории обобщенных функций. Данный подход упирается в
проблему умножения разрывных функций на обобщенные, которая
возникает в слагаемом
![]() .
.
В работах [45,46,47] в рамках секвенциального подхода
теории обобщенных функций [1] вводится определение
произведения двух распределений ![]() как предела
последовательности
(если такой предел существует в смысле теории
распределений)
как предела
последовательности
(если такой предел существует в смысле теории
распределений)
![]() , где ``
, где ``![]() '' -
свертка функций
'' -
свертка функций ![]() и
и ![]() а
а ![]() -
-
![]() -последовательность гладких функций, т.е.
-последовательность гладких функций, т.е.
![]() сходится к
сходится к ![]() -функции (опять же, в смысле теории
распределений). Из этого определения, в частности, следует, что
-функции (опять же, в смысле теории
распределений). Из этого определения, в частности, следует, что
В работах [11,12] предложено другое определение
произведения распределений, основанное на распространении
классической формулы дифференцирования произведения на случай
распределений. Данный подход позволил решить ряд задач об
оптимальном импульсном управлении межорбитальными космическими
перелетами [11], механики жидкости [10],
математической экономики [13]. Cогласно [12], если
![]() - ``согласованная пара'', то
- ``согласованная пара'', то
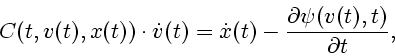
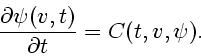
Сравнивая (1.6), (1.7), (1.10) и (1.11), убеждаемся, что разные определения решения приводят к разным решениям одного и того же уравнения. Этот эффект O.Хайек в [43] назвал парадоксом дифференциальных уравнений.
К результатам, аналогичным только что рассмотренным, приводит конструкция, предложенная в работе [50].
Кроме перечисленных работ следует обратить внимание на статьи
[7,8], где в рамках секвенциального подхода теории
обобщенных функций для сингулярно возмущенных систем выработан
подход, родственный рассмотренному в [12] и рассчитанный
на ступенчатые вектор-функции ![]() .
.
Я.Курцвейль в работе [44] предлагает в качестве решения
системы дифференциальных уравнений, содержащей ![]() -функцию
в качестве сомножителя (другой сомножитель зависит от фазовых
переменных), рассматривать предел последовательности абсолютно
непрерывных решений системы дифференциальных уравнений, в
которой
-функцию
в качестве сомножителя (другой сомножитель зависит от фазовых
переменных), рассматривать предел последовательности абсолютно
непрерывных решений системы дифференциальных уравнений, в
которой ![]() -функция заменена последовательностью ее
гладких аппроксимаций. Естественность построения обобщенных
решений при помощи предельного перехода с точки зрения теории
управления отмечалась в [17].
-функция заменена последовательностью ее
гладких аппроксимаций. Естественность построения обобщенных
решений при помощи предельного перехода с точки зрения теории
управления отмечалась в [17].
Этот подход получил свое развитие в [19], где для
линейного дифференциального уравнения ![]() -го порядка с
обобщенными коэффициентами было получено достаточное условие,
обеспечивающее независимость предела последовательности гладких
решений от выбранного способа аппроксимации обобщенных
коэффициентов последовательностями гладких функций.
-го порядка с
обобщенными коэффициентами было получено достаточное условие,
обеспечивающее независимость предела последовательности гладких
решений от выбранного способа аппроксимации обобщенных
коэффициентов последовательностями гладких функций.
Далее, в монографии [15] указаны условия (типа Фробениуса) единственности предельных решений и выписано их представление в классических терминах для воздействий, представленных обобщенными производными локально интегрируемых функций. Формулировка результата о предельном переходе в нелинейной системе дифференциальных уравнений с воздействием - обобщенной производной функции ограниченной вариации - впервые была опубликована в [22]. Полное доказательство этого результата вышло в [27] и позже, с использованием другой техники, в [25].
Отметим, что в работе [27] техника разрывной замены времени была разработана для построения замыкания множества обычных траекторий в отличие от [21], где техника разрывной замены развивалась для замыкания множества траекторий, порожденных чисто импульсными управлениями. Это позволило рассмотреть не только ``корректный'' случай (когда из сходимости последовательности, аппроксимирующей обобщенные функции, входящие в систему, следует сходимость соответствующей последовательности решений), но и случай, когда последовательность решений системы дифференциальных уравнений, порожденная гладкими аппроксимациями обобщенных функций, сходящейся не является, и описать все частичные пределы этой последовательности [28,29,30,31,23].
В дополнение к перечисленным работам следует отметить работу
[6], где с помощью квазидифференциальных уравнений
исследуется линейное дифференциальное уравнение ![]() -го порядка
с обобщенными коэффициентами. Из работ, вышедших в последнее
время, представляет интерес работа [24], где исследуется
вопрос определения разрывного решения без предположения
мультипликативного вхождения обобщенного воздействия в правую
часть системы.
-го порядка
с обобщенными коэффициентами. Из работ, вышедших в последнее
время, представляет интерес работа [24], где исследуется
вопрос определения разрывного решения без предположения
мультипликативного вхождения обобщенного воздействия в правую
часть системы.
Далее будет обсуждаться подход, базирующийся на аппроксимации обобщенных воздействий обычными (суммируемыми) функциями. Дело в том, что импульсные системы часто возникают как системы первого приближения для систем с ограниченным, но достаточно большим воздействием (часто это управляющее воздействие). Примеры таких систем мы можем наблюдать в механике космического полета [20], где управляющие воздействия большой интенсивности действуют на объект в течение нескольких секунд или минут, а процесс управления продолжается в течение нескольких часов, дней или даже недель, электрофизике, практике медицинского лечения (разовое применение лекарства достаточно быстро приводит к изменению состояния организма) и так далее, а также в результате расширения вариационных задач в теории оптимального управления [4,9,14,15,23,26].