Приведем примеры управляемых систем, в которых функция цены
Приведем примеры управляемых систем, в которых функция цены
![]() построена как обобщенное решение задачи
Коши (2.1). При этом в АС использовался КРО
построена как обобщенное решение задачи
Коши (2.1). При этом в АС использовался КРО
![]() (5.2), который для случая, когда функция
(5.2), который для случая, когда функция
![]() задана на сетке, а гамильтониан
задана на сетке, а гамильтониан ![]() - кусочно-линейная
положительно однородная функция по переменной
- кусочно-линейная
положительно однородная функция по переменной ![]() ,
вычисляется как последовательный максимум (см. (4.2)).
Вычисление выполняется следующим образом:
,
вычисляется как последовательный максимум (см. (4.2)).
Вычисление выполняется следующим образом:
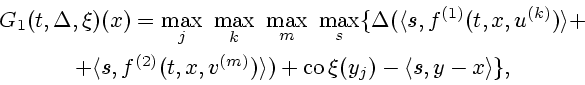
В этой формуле ![]() - вершины многогранника
- вершины многогранника
![]() в дифференциальной игре (2.2)-(2.3),
в дифференциальной игре (2.2)-(2.3), ![]() - конусы линейности
функции
- конусы линейности
функции
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
,
![]() - количество вершин многогранника
- количество вершин многогранника
![]() .
.
Аналогично, ![]() - вершины многогранника
- вершины многогранника
![]() и
и
![]() - конусы линейности функции
- конусы линейности функции
![]() ,
т.е.
,
т.е.
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() - количество вершин многогранника
- количество вершин многогранника
![]() .
.
Множество
![]() - выпуклый многогранник - есть
пересечение субдифференциала
- выпуклый многогранник - есть
пересечение субдифференциала
![]() ,
вычисленного в узле
,
вычисленного в узле ![]() , принадлежащем
, принадлежащем
окрестности
![]() узла
узла ![]() ,
с конусом линейности гамильтониана
,
с конусом линейности гамильтониана ![]() . Максимизируемая
функция здесь линейна по переменной
. Максимизируемая
функция здесь линейна по переменной ![]() . Поэтому вычисление
значения
. Поэтому вычисление
значения
![]() оператора
оператора ![]() в точке
в точке ![]() редуцируется к конечной совокупности задач линейного программирования.
редуцируется к конечной совокупности задач линейного программирования.
П р и м е р 1. Тестовый пример [15]. Рассматривается дифференциальная игра
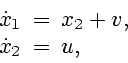
Численное моделирование осуществляется в точке
![]() в момент
в момент ![]() .
Точка
.
Точка ![]() находится на пересечении сингулярных линий функции
находится на пересечении сингулярных линий функции
![]() . Известно, что
. Известно, что
![]() . Ниже
приведены параметры вычислительной схемы и отвечающие им
приближенные значения
. Ниже
приведены параметры вычислительной схемы и отвечающие им
приближенные значения ![]() решения в точке
решения в точке ![]()
1)
![]()
2)
![]()
3)
![]()
Здесь ![]() и
и ![]() - шаги разбиения пространства
- шаги разбиения пространства ![]() по переменным
по переменным ![]() и
и ![]() соответственно.
соответственно.
П р и м е р 2. Рассматривается математическая модель управления движением
маятника в вязкой среде
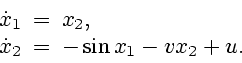
Аналитическое решение задачи неизвестно. Сопоставление
результатов ведется с результатами счета, полученными по другой
методике [14], позволяющей строить аппроксимации множеств
уровня функции цены. Ниже приведены точки ![]() ,
в которых велся счет, параметры вычислительной схемы и
отвечающие им приближенные значения
,
в которых велся счет, параметры вычислительной схемы и
отвечающие им приближенные значения ![]() решения, а также
приближенные значения
решения, а также
приближенные значения ![]() , полученные посредством
конструирования множеств уровня функции цены.
, полученные посредством
конструирования множеств уровня функции цены.
1)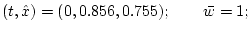
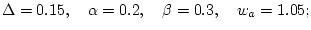
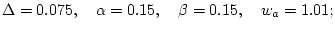
2)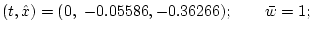
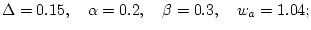
Поступила 25.09.99