4. Операторы шага

Здесь рассматриваются аппроксимации форм ОСП на шаге $\Delta$ разбиения временного отрезка. В частности, показывается, что при достаточно больших значениях параметра $c$, отвечающие им разностные формы ОСП позволяют приближенно вычислять приращения $w(t+\Delta,x)-w(t,x)$ по времени функции $w$ в точке $x$. Причем разные формы оператора дают одинаковый результат.

Введем в рассмотрение коническое множество в пространстве переменных $t,x$:

$$\bar{D} = \{ (t,x) \in [0,\vartheta] \times R^n: \ t \in [t_0, \vartheta], \ x \in (\hat{x}+(t-t_0) \cdot F)\},$$

где $t_0 = \max \{0, \vartheta - \hat{r}/K \}$.

По построению следует, что

1) множество $\bar{D}$ сильно инвариантно относительно дифференциального включения $\dot{x} \in F$, следовательно, $\bar{D} \subset D$;

2) сечение $\bar{D}(t)$ множества $\bar{D}$ в каждый момент $t$ является шаром с центром в точке $\hat{x}$ радиуса $r=r(t)=\hat{r} -(\vartheta -t) K$.

Описываемые ниже конструкции, связанные с изучением свойств семейства форм $\{ \pi^c (\cdot), \ \ c \geq 0 \}$ ОСП, рассматриваются ``над'' множест-
вом $\bar{D}.$

О п р е д е л е н и е 4. Пусть $t \in [t_0, \vartheta)$, $\Delta > 0$, $(t+\Delta) \in [t_0, \vartheta]$, параметр $c \geq 0$. Оператором шага $\pi^c_{\Delta}(\cdot)$ назовем отображение $2^{R^{n+1}} \rightarrow 2^{R^{n+1}}$, заданное соотношениями

$$\pi^c_{\Delta}(B) = \{ z_* \in R^{n+1}: \ B \bigcap \widetil... ...elta; t, z_*,l) \neq \emptyset \ \ \forall\, l \in S_{n+1} \}.$$

Здесь $B \subset R^{n+1}, \ \widetilde {Z}^c(t+\Delta; t,z_*,l)= z_* +\Delta \cdot F^c(t,z_*,l)$.

Будем полагать, что операторы эквивалентны, если совпадают порождаемые ими множества. Сформулируем условия, при которых операторы шага из совокупности $\{ \pi^c_{\Delta}, \ c \geq 0 \}$ действуют эквивалентным образом. Приведем определение локально-выпуклой оболочки функции.

О п р е д е л е н и е 5. Пусть $\phi$ - функция, определенная на множестве $\bar{D}(t+\Delta) \subset R^n$. Рассмотрим сужение $\phi_{O(x,K \Delta)}$ функции $\phi$ на шар
$O(x, K \Delta) = \{y \in R^n: \ \Vert y-x\Vert \leq K \Delta \}$, $x \in \bar{D}(t)$. Локально-выпуклой оболочкой (ЛВО) функции $\phi_{O(x,K \Delta)}$ называется функция $\mathrm{co\,}\phi$, заданная формулой

$$\mathrm{co\,}\phi (y)= \inf \left\{ \sum^{n+1}_{i=1} \alpha_i \phi (y^{(i)}): \right.$$

$$\left. \alpha_i \geq 0, i=1,\ldots,n+1; \ \sum^{n+1}_{i=1} \... ...=1} \alpha_i y^{(i)} =y, \ y^{(i)} \in O(x, K\Delta) \right\}.$$

Здесь подчеркнем, что ЛВО функции $\phi$ определяется двумя параметрами: точкой $x \in \bar{D}(t)$ и числом $K \Delta$, которое является радиусом шара с центром в точке $x$. При обозначении ЛВО указание на эти параметры для краткости опущено.

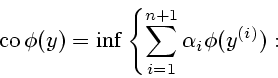
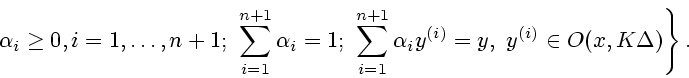
Определим функции $\bar{\psi}^c_{\Delta}(\cdot): \ \bar{D}(t) \rightarrow R, \ c \geq 0$

$$\bar{\psi}^c_{\Delta}(x) = \inf \{ \xi: \ (x,\xi) \in \pi^c_... ...lta} (\mathrm{epi\,}\ \mathrm{co\,}\phi_{O_{K \Delta}(x)}) \}.$$

Формулируемая ниже теорема использует результаты работы [13], вытекает из условий (F1)-(F2), определения ЛВО и теорем об отделимости выпуклого анализа.

Теорема 4.1   Если $\phi: \ \bar{D}(t+ \Delta) \rightarrow R$ - функция, удовлетворяющая условию Липшица с константой $\lambda, \ x \in\bar{D}(t)$, то для любого $c \geq 2 \lambda K$, для любого достаточно малого числа $\Delta > 0$ имеют место равенства

$$\pi^c_{\Delta} (\mathrm{epi\,}\ \phi_{O(x,K \Delta)}) = \pi^... ...\,}\phi) = \pi^o_{\Delta} (\mathrm{epi\,}\ \mathrm{co\,}\phi).$$

Теорема, в частности, утверждает, что при любом $c \geq 2 \lambda K$ имеют место равенства

$$\psi^c_{\Delta}(x) = \bar{\psi}^c_{\Delta}(x) = \bar{\psi}^o_{\Delta}(x), \quad x \in \bar{D}(t).$$

Справедливо представление

$$\psi^c_{\Delta}(x) = \max_{s \in S_n} \min_{f \in F_1(t,x,s)... ...+ \Delta f), \quad x \in \bar{D}(t), \quad c \geq 2 \lambda K.$$ (4.1)

Обоснование равенства (4.1) приведено в работе [16], оно опирается на определения операторов шага и семейств отображений (3.3).

Среди свойств максимина от ЛВО функции укажем то из них, которое позволяет перейти непосредственно к численным реализациям.

Пусть функция $\phi (\cdot): \ \bar{D} (t+ \Delta) \rightarrow R$ удовлетворяет условиям теоремы 1, тогда для построения функций $\psi^c_{\Delta}(\cdot): \ \bar{D}(t) \rightarrow R$ при $c \geq 2 \lambda K$ применима формула

$$\psi^c_{\Delta}(x) = \max_{y \in O(x,K_0 \Delta)} \max_{s \i... ... \{ \Delta h(t,x,s) + \l s, x-y \r + \mathrm{co\,}\phi (y) \},$$ (4.2)

где $x \in \bar{D}(t)$;

$\partial \mathrm{co\,}\phi (y) = \{ s \in R^n: \ \mathrm{co\,}\phi (y^*) - \mathrm{co\,}\phi (y) \geq \l s, y^*-y \r\forall\, y^* \in O(x,K \Delta) \}$ - субдифференциал ЛВО функции $\phi$, вычисленный в точке $y \in O(x, K_0 \Delta)$. Константа $K$ (3.2) выбрана из условия

$$\max_{(t,u,v) \in [t_0,\vartheta] \times P \times Q} \Vert f(t,x,u,v) \Vert \leq K_0 < K/2.$$

Вывод формулы (4.2) осуществляется средствами выпуклого анализа, опирается на критерий минимума выпуклой функции при наличии выпуклых ограничений и определение семейства (3.3).