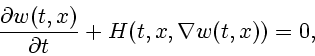 |
(2.1) |
Рассматривается задача Коши для уравнения Гамильтона-Якоби
Исследование проблемы приближенного построения обобщенного решения задачи (2.1) ведется в контексте дифференциальной игры
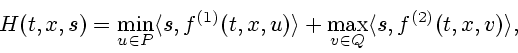
Правая часть ![]() системы (2.2) удовлетворяет следующим
условиям.
системы (2.2) удовлетворяет следующим
условиям.
(f1) Функция ![]() непрерывна по совокупности переменных.
непрерывна по совокупности переменных.
(f2) Функция ![]() удовлетворяет условию Липшица по переменной
удовлетворяет условию Липшица по переменной ![]()
(f3) Существует константа
![]() такая, что
выполняется неравенство
такая, что
выполняется неравенство
Условия (f1)-(f3) и вид правой части системы (2.2) определяют
следующие свойства гамильтониана ![]() .
.
(H1) Имеет место равномерная непрерывность на любом компакте
в пространстве переменных ![]() ,
, ![]() ,
, ![]() .
.
(H2) Выполняется условие Липшица по переменной ![]()
(H3) Выполняется условие Липшица по переменной ![]()
(H4) Гамильтониан положительно однороден по переменной ![]()
Показателем качества дифференциальной игры является
терминальный функционал
Функционал ![]() ставит в соответствие реализовавшемуся движению
ставит в соответствие реализовавшемуся движению
![]() число
число
![]() .
.
При указанных условиях (f1)-(f3) на правую часть системы
(2.2) существует функция цены
![]() дифференциальной игры
(2.2)-(2.3). При этом функция цены совпадает с обобщенным
решением задачи Коши (2.1) для случая, когда гамильтониан
дифференциальной игры
(2.2)-(2.3). При этом функция цены совпадает с обобщенным
решением задачи Коши (2.1) для случая, когда гамильтониан ![]() удовлетворяет условиям (H1)-(H4). Обобщенное решение задачи
(2.1) здесь однозначно определяется краевым условием и парой
дифференциальных неравенств
удовлетворяет условиям (H1)-(H4). Обобщенное решение задачи
(2.1) здесь однозначно определяется краевым условием и парой
дифференциальных неравенств
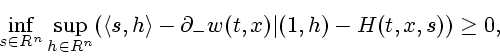
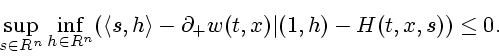
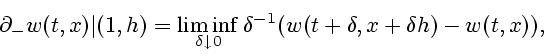
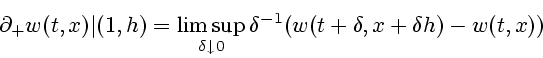
Эквивалентность функции цены дифференциальной игры и обобщенного решения задачи (2.1) позволяет применять при построении обобщенных решений УГЯ конструкции теории дифференциальных игр.
Функция цены - единственная функция, которая при
заданной плате (2.3) удовлетворяет одновременно
свойствам ![]() - и
- и ![]() -стабильности.
Свойство
-стабильности.
Свойство ![]() -стабильности (
-стабильности (![]() -стабильности) означает слабую
инвариантность
-стабильности) означает слабую
инвариантность
надграфика (подграфика) функции цены
относительно некоторого семейства дифференциальных включений
- семейства характеристических
включений для (2.1).
Построение слабо инвариантного множества может быть
осуществлено с помощью известного в теории дифференциальных
игр оператора стабильного поглощения (ОСП). Следует
отметить, что существует определенный произвол в выборе
семейства характеристических включений, что используется
ниже при построении ОСП.