Рассмотрим функции, построенные на основе операторов шага
![]() ,
, ![]() .
Пусть заданы разбиение
.
Пусть заданы разбиение
![]() отрезка
отрезка
![]() и
функция
и
функция
![]() .
Определим отвечающие этому разбиению функции
.
Определим отвечающие этому разбиению функции
Определим разностный оператор ![]() по формуле
по формуле
Определим также оператор последовательного максимина локально-выпуклых оболочек.
О п р е д е л е н и е 6. Пусть
![]() - разбиение отрезка
- разбиение отрезка
![]() ,
,
![]() - произвольная функция, определенная на
- произвольная функция, определенная на
![]() .
Оператором последовательного максимина (ОПМ) назовем оператор
.
Оператором последовательного максимина (ОПМ) назовем оператор
![]()
![]()
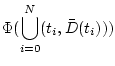 ,
,
![]() , заданный соотношениями
, заданный соотношениями
Справедлива теорема
Результат может быть усилен [17], если на гамильтониан ![]() (и
соответственно на семейство (3.3) многозначных
отображений) наложить условие Липшица по переменной
(и
соответственно на семейство (3.3) многозначных
отображений) наложить условие Липшица по переменной ![]() .
.
(H5) Существует число
![]() такое, что для любых
такое, что для любых
![]() ,
,
![]() ,
любом
,
любом ![]() имеет место неравенство
имеет место неравенство
(F5) Существует число
![]() такое, что
для любых
такое, что
для любых
![]() ,
,
![]() ,
любом
,
любом ![]() имеет место неравенство
имеет место неравенство
В этом случае может быть оценена сходимость ОПМ.
Действительно, оператор
![]() , определяемый
формулой (5.2), удовлетворяет [8] следующим
условиям:
, определяемый
формулой (5.2), удовлетворяет [8] следующим
условиям:
(G1) Совместимость
(G2) Непрерывность отображения
![]()
(G3) Коммутативность
(G4) Ограниченность
(G5) Монотонность
(G6) Экспоненциальное возрастание
(G7) Условие Липшица по переменной ![]()
(G8) Условие аппроксимации
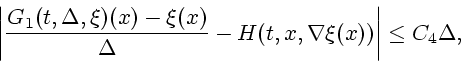
Как известно [8], АС с оператором, удовлетворяющим условиям
(G1)-(G8), сходится к обобщенному решению ![]() задачи
Коши (2.1) со скоростью, пропорциональной
задачи
Коши (2.1) со скоростью, пропорциональной ![]() .
.