Выше приведена АС построения обобщенного решения задачи
(2.1). При этом использован ОСП, известный в теории
дифференциальных игр и примененный здесь к решению задачи 1 - задачи о
построении надграфика обобщенного решения. Аналогичным
образом ОСП используется при решении задачи 2 - задачи о
построении подграфика ![]() . При этом получаем КРО
. При этом получаем КРО ![]() ,
двойственный по отношению к КРО
,
двойственный по отношению к КРО ![]() и определяемый по
формуле
и определяемый по
формуле
Отметим, что оператор ![]() допускает следующее представление
допускает следующее представление
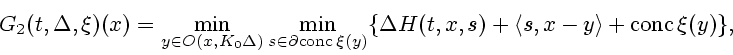
![\begin{displaymath}
\max_{(t,u,v) \in [t_0, \vartheta] \times P
\times Q} \Vert f(t,x,u,v)\Vert \leq K_0 < {K\over 2}.
\end{displaymath}](img262.gif)
З а м е ч а н и е. Формулы (5.2) и (6.1) для операторов ![]() и
и
![]() , соответственно, можно интерпретировать как обобщение
формул Хопфа [23] на ЛВО (ЛВГО) функций.
Более точно, справедливы равенства
, соответственно, можно интерпретировать как обобщение
формул Хопфа [23] на ЛВО (ЛВГО) функций.
Более точно, справедливы равенства
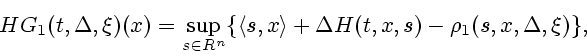
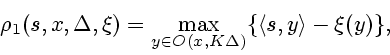
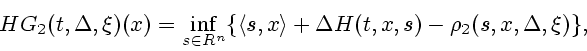
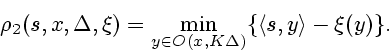
Оператор ![]() , как и оператор
, как и оператор ![]() , удовлетворяет
условиям (G1)-(G8), следовательно, порожденная им АС
сходится к обобщенному решению
, удовлетворяет
условиям (G1)-(G8), следовательно, порожденная им АС
сходится к обобщенному решению ![]() задачи Коши (2.1)
со скоростью, пропорциональной
задачи Коши (2.1)
со скоростью, пропорциональной ![]() . Поэтому любая
выпуклая комбинация операторов
. Поэтому любая
выпуклая комбинация операторов ![]() и
и ![]() , определяемая
формулой
, определяемая
формулой
Отметим, что среди КРО вида (6.2) существует оператор, определяющий квазидифференцируемую (в смысле Демьянова [24]) функцию, аппроксимирующую обобщенное решение задачи (2.1).
Рассмотрим КРО на множестве таблично заданных функций.
Пусть
![]() (i=1, ...,n) - шаги
дискретизации фазового пространства. Совокупность точек
(i=1, ...,n) - шаги
дискретизации фазового пространства. Совокупность точек
![]() таких, что
таких, что
![]()
![]() ,
назовем сеткой и будем обозначать
,
назовем сеткой и будем обозначать
![]() .
Здесь
.
Здесь
![]() - орты в
- орты в ![]() .
Пусть
.
Пусть ![]() - выпуклая оболочка сетки
- выпуклая оболочка сетки
![]() :
:
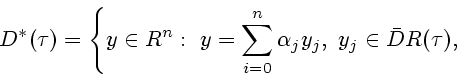
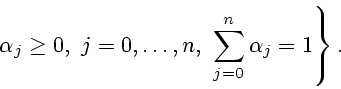
Полагаем, что
![]() и
и
![]() - функция, удовлетворяющая
условию Липшица. Пусть
- функция, удовлетворяющая
условию Липшица. Пусть ![]() - некоторое фиксированное
разбиение n-мерного куба на симплексы.
- некоторое фиксированное
разбиение n-мерного куба на симплексы.
Определим значение оператора
![]() в точке
в точке ![]() соотношением
соотношением
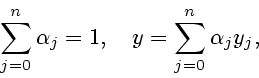
АС с КРО ![]() также сходится [18] со скоростью,
пропорциональной шагу
также сходится [18] со скоростью,
пропорциональной шагу ![]() разбиения отрезка
разбиения отрезка
![]() . Здесь подчеркнем, что оператор
. Здесь подчеркнем, что оператор
![]() может быть использован для реального (численного)
построения аппроксимации решения задачи (2.1).
может быть использован для реального (численного)
построения аппроксимации решения задачи (2.1).
Рассмотрим еще один оператор, который непосредственно применим при численных построениях. Этот оператор имеет очень простую структуру, полученную с помощью метода наименьших квадратов, поэтому его можно использовать для быстрых вычислений.
Пусть
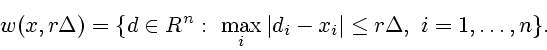
Пусть
![]() - линейная функция, наиболее близкая в
смысле квадратичного отклонения к табличной функции
- линейная функция, наиболее близкая в
смысле квадратичного отклонения к табличной функции
![]() ,
т.е. параметры
,
т.е. параметры
![]() определяются из условия минимума квадратичного отклонения
определяются из условия минимума квадратичного отклонения
![\begin{displaymath}
\sum_{l=1}^m [\xi(y_l) - (\l a,y_l \r +b)]^2.
\end{displaymath}](img308.gif)
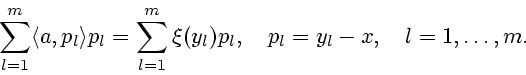
Система (6.4) является симметрической и может быть
записана в виде
Симметрия множества
![]() относительно
координатных плоскостей обеспечивает диагональность системы
(6.5)
относительно
координатных плоскостей обеспечивает диагональность системы
(6.5)
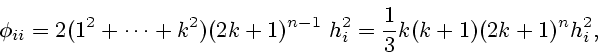
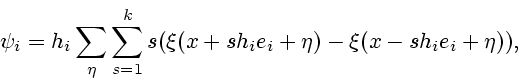
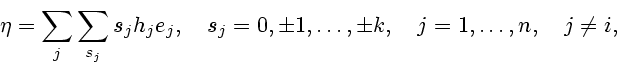
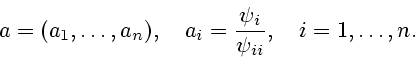
Можно проверить, что линейная функция ![]() , рассмотренная на
шаре
, рассмотренная на
шаре
![]() , расположена между ЛВО и ЛВГО функции
, расположена между ЛВО и ЛВГО функции ![]() ,
построенными на шаре
,
построенными на шаре ![]() ,
, ![]()
Отметим следующий факт. Пусть
![]() . Тогда
КРО
. Тогда
КРО ![]() обращается в оператор Лакса-Фридрихса [17].
обращается в оператор Лакса-Фридрихса [17].
![\begin{displaymath}
\xi_0= \frac{1}{2n+1} [\xi (x) + \sum_{i=1}^n (\xi(x+ \Delta
\gamma_i e_i)+ \xi(x- \Delta \gamma_i e_i))].
\end{displaymath}](img329.gif)