Ниже приводится описание ОСП, примененного здесь для
построения обобщенного решения задачи (2.1).
Приводимая в работе конструкция предполагает построение сужения функции
![]() на ограниченное множество. В качестве этого множества выбирается
стабильный мост
на ограниченное множество. В качестве этого множества выбирается
стабильный мост
![]() в конфликтной задаче
сближения с шаром
в конфликтной задаче
сближения с шаром
О п р е д е л е н и е 1. Многозначное отображение
Отметим, что при указанных предположениях на правую часть уравнения
(2.2)
семейство многозначных отображений
(F1) Для любых
![]() множество
множество ![]() выпукло, замкнуто и удовлетворяет вложению
выпукло, замкнуто и удовлетворяет вложению
![]() .
.
(F2) Для любых
![]() справедливо соотношение
справедливо соотношение
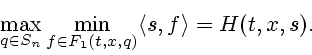
(F3) Для отображения
![]() существует функция
существует функция
![]()
![]() ,
,
![]() при
при
![]() такая, что
такая, что
Здесь
![]() - хаусдорфово расстояние между множествами
- хаусдорфово расстояние между множествами
![]() и
и ![]() .
.
(F4) Существует число
![]() такое, что для любых
такое, что для любых
![]() и любого
и любого ![]() имеет место неравенство
имеет место неравенство
Отметим еще один факт. Непрерывная функция ![]() является функцией
цены дифференциальной игры (2.2)-(2.3) тогда и только тогда,
когда множество
является функцией
цены дифференциальной игры (2.2)-(2.3) тогда и только тогда,
когда множество
![]() является стабильным мостом в задаче сближения с целевым множеством
является стабильным мостом в задаче сближения с целевым множеством
![]() , решаемой игроком, распоряжающимся
управлением
, решаемой игроком, распоряжающимся
управлением ![]() (управлением
(управлением ![]() ) для расширенной системы
) для расширенной системы
Утверждение остается в силе, когда рассматривается сужение функции
![]() на стабильный мост
на стабильный мост ![]()
В дальнейшем задачу о построении надграфика сужения функции
![]() на множество
на множество ![]() будем называть задачей 1,
а задачу о построении подграфика сужения функции на это множество -
задачей 2. Подходы к решению каждой из задач близки, поэтому
описание построений приведем для одной из них - для задачи 1.
будем называть задачей 1,
а задачу о построении подграфика сужения функции на это множество -
задачей 2. Подходы к решению каждой из задач близки, поэтому
описание построений приведем для одной из них - для задачи 1.
Введем обозначения.
Рассмотрим дифференциальную игру для расширенной динамической системы
Максимальный стабильный мост ![]() для задачи сближения
(3.5)-(3.6)
является решением задачи 1.
для задачи сближения
(3.5)-(3.6)
является решением задачи 1.
Гамильтониан динамической системы (3.5)
зададим равенством
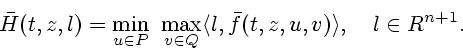
Символом ![]() обозначим множество векторов
обозначим множество векторов
![]() .
.
Построим прямое произведение множества ![]() и отрезка
и отрезка ![]()
В пространстве переменных ![]() выделим область
выделим область
![]() , априори содержащую
, априори содержащую ![]() .
.
Введем в рассмотрение совокупность семейств многозначных отображений,
зависящих от параметра
![]()
Здесь
![]() .
.
Условия (F1)-(F4) для семейства отображений (3.3) влекут
аналогичные условия для любого семейства отображений (3.7).
Имеют место условия ![]() -
-![]() .
.
![]() Для любых
Для любых ![]() ,
,
![]() множество
множество ![]() выпукло, замкнуто и содержится в
выпукло, замкнуто и содержится в ![]() .
.
![]() Для любых
Для любых ![]() ,
,
![]() справедливо неравенство
справедливо неравенство
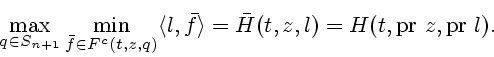
![]() Для любого
Для любого ![]() для отображения
для отображения
![]() существует константа
существует константа ![]() такая, что
такая, что
![]() Для любого
Для любого ![]() существует константа
существует константа
![]() такая, что для любых
такая, что для любых
![]() и любого
и любого ![]() имеет место неравенство
имеет место неравенство
Известно [14], что любое семейство отображений,
удовлетворяющее условиям типа ![]() -
-![]() ,
индуцирует ОСП для соответствующей задачи сближения.
,
индуцирует ОСП для соответствующей задачи сближения.
О п р е д е л е н и е 2. Отображение
Здесь
![]() - множество всех точек из
- множество всех точек из ![]() ,
в которые в момент
,
в которые в момент ![]() приходят решения
приходят решения
![]() дифференциального включения
дифференциального включения
![]() при фиксированном значении
при фиксированном значении
параметра ![]() .
.
О п р е д е л е н и е 3. Множество ![]() называется стабильным мостом в
задаче 1 сближения
с замкнутой целью
называется стабильным мостом в
задаче 1 сближения
с замкнутой целью
![]() , если выполняются условия:
, если выполняются условия:
1)
![]() ,
,
2)
![]() .
.
Наибольший по включению стабильный мост называется максимальным стабильным мостом.
Таким образом описано семейство
Семейство дифференциальных включений с правыми частями
из (3.7) (при любом
фиксированном ![]() ) называется характеристическим семейством для задачи
(2.1). Сказанное означает, что для любой точки
) называется характеристическим семейством для задачи
(2.1). Сказанное означает, что для любой точки
![]()
![]()
![]() ,
,
![]() ,
принадлежащей графику обобщенного решения задачи Коши для УГЯ, для любого
,
принадлежащей графику обобщенного решения задачи Коши для УГЯ, для любого
![]() , для любого момента
, для любого момента ![]() ,
,
![]() ,
существует решение
,
существует решение ![]() дифференциального включения
дифференциального включения
![]() ,
, ![]() такое, что точка
такое, что точка ![]() принадлежит графику обобщенного решения,
т.е.
принадлежит графику обобщенного решения,
т.е.
![]() .
.