4. Уравнение Гамильтона-Якоби (Беллмана)

Определим гамильтонианы (i=1,2), где следующим образом:





и функцию

Далее будет доказано, что функция цены V является единственным вязким решением на множестве уравнения

(где - градиент функции V), называемого уравнением Гамильтона-Якоби (Беллмана) (далее для краткости будем называть его уравнением Гамильтона-Якоби). Аппарат вязких решений, используемый ниже, восходит к работам [5], [8]. Аналогичный подход к задачам оптимизации используется в [7], [9]. Существенным отличием данной работы являются более общий вид функционала, а также возможность отказа от вспомогательнной задачи импульсного расширения (см. [9]).

Приведем из [8] определение вязкого решения. Нам понадобятся следующие обозначения: если то

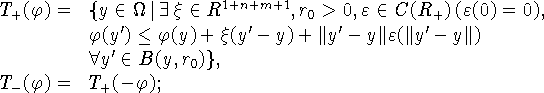
если (соответственно ), то

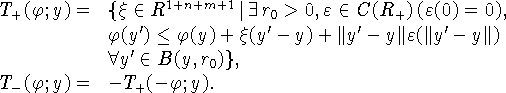
(Множества и называются, соответственно, супер- и субдифференциалами функции в точке , а их элементы - супер- и субградиентами).

Определение 4.1. Непрерывная на множестве функция называется вязким верхним (нижним) решением уравнения , если



функция удовлетворяющая одновременно и , называется вязким решением .

Теорема 4.1. Пусть выполнены условия (А) и (Б). Тогда

функция цены V есть единственное вязкое решение на множестве уравнения ;

V удовлетворяет краевым условиям и .

Доказательство. Покажем сначала, что V - нижнее решение. Пусть и т.е., существуют число и непрерывная на функция такие, что

для всех Ясно, что функция F(y) дифференцируема в точке и

Из второго равенства метода динамического программирования мы имеем для всех

Перенесем в правую часть неравенства, разделим обе части на и устремим к нулю. Нетрудно убедиться в том, что при для всех В силу дифференцируемости функции F в точке получаем:

Осталось показать, что Пусть на . Из (3.1) для любого мы имеем:

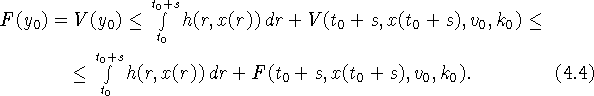
Заметим, что для подобных управлений траектория есть решение задачи Коши

Разделим неравенство (4.4) на s и устремим s к нулю, получая

что и требовалось доказать.

Остается проверить, что V - верхнее решение уравнения (4.1). Пусть и пусть т.е., существуют число и непрерывная на функция такие, что

для всех Требуется доказать, что либо либо

Из (3.2) мы имеем:

для некоторых Допустим, т.е. импульсное управление оптимально. Пользуясь следствием 1 из Леммы 3.1, получаем для всех

Следовательно,

Как и раньше, разделим на и в пределе при получим:

Используя обратный ход рассуждений, из неравенства

получаем

для всех Иными словами, оптимальное управление непрерывно на интервале для некоторого

Покажем, что если справедливо (4.5), то

Предположим противное, т.е.

Пусть - оптимальное непрерывное на управление; введем обозначение и рассмотрим разность Согласно (4.6) и свойствам интеграла Лебега-Стилтьеса [4], справедливо следующее:



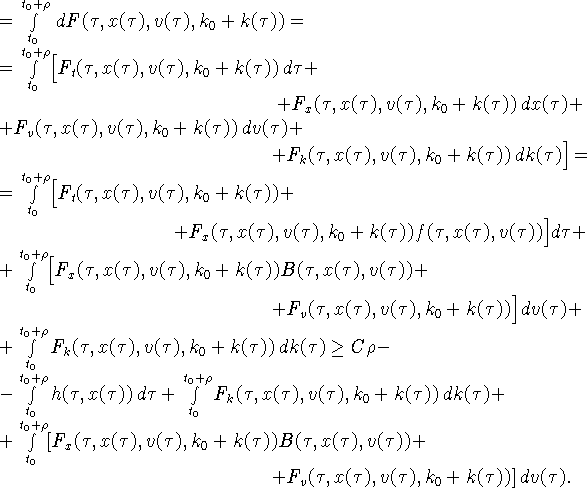
Введем обозначения: пусть

и

Рассмотрим интеграл

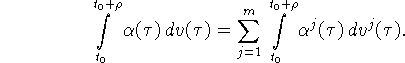
Разобьем интервал на подинтервалы так, чтобы на каждом из указанных подинтервалов все компоненты вектор-функции были монотонны. Тогда для всех мы имеем:

где если не убывает на ( если не возрастает на ), и

Справедливо следующее равенство:

где - некоторая непрерывная функция, причем для всех

Положим Тогда

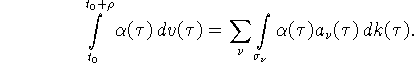
Следовательно,

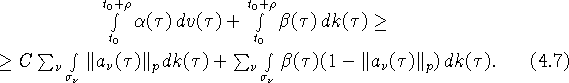
Нетрудно проверить, что обе суммы в (4.7) неотрицательны. Таким образом,



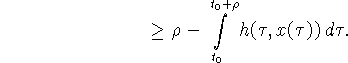
Поскольку то



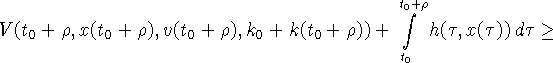
Данное неравенство противоречит оптимальности управления на т.е. что и требовалось доказать.

Остается отметить, что уравнение (4.1) удовлетворяет требованиям теорем единственности решения уравнения Гамильтона-Якоби (см., например, [5], [6], [8]).

Теорема доказана.

Предложение 4.1. Уравнение эквивалентно в смысле теории вязких решений уравнению

где

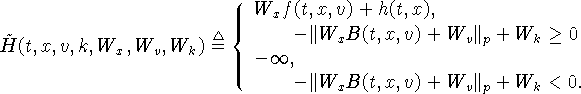
Доказательство. Далее будем пользоваться эквивалентным определением вязкого решения, использующим приближение с помощью гладких функций (см., например, [7], [9]).

Пусть функция V - вязкое решение (4.1) на множестве . Очевидно, что в этом случае V является нижним решением для (4.8) на . Остается проверить, что V есть верхнее решение (4.8). Итак, пусть функция - гладкая и достигает локального минимума, равного нулю, в точке Тогда по определению вязкого решения,

где



Если то Значит, по определению гамильтониана V - верхнее решение в точке уравнения (4.8). С другой стороны, пусть Тогда исходя из (4.8), мы имеем: Следовательно, V - вязкое верхнее решение (4.8) на всем множестве

Тот факт, что вязкое решение (4.8) является вязким решением (4.1), доказывается аналогично.

Поскольку решения V и W уравнений (4.1) и (4.8) единственны на множестве они тождественно совпадают в этой области.

Предложение 4.1 доказано.

Следствие 1. Помимо и , функция цены V удовлетворяет в смысле теории вязких решений уравнению

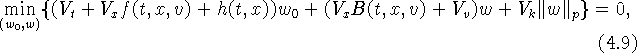
где и

Уравнение (4.9) подробно изучалось в работе [9].

Замечание. Уравнения (4.1), (4.8) и (4.9) позволяют в некоторых случаях судить об оптимальности того или иного управления. Допустим W(y)=W(t,x,v,k) - произвольное вязкое решение уравнения Гамильтона-Якоби на множестве , удовлетворяющее краевому и граничному условиям (2.7) и (2.8).

a) Пусть - точка дифференцируемости функции W(y). Если то постоянное управление оптимально на некотором интервале s>0. Если то скачок управления в момент является оптимальным.

б) Пусть - точка субдифференцируемости функции W(y), - субградиент. Если то постоянное управление является оптимальным на некотором интервале s>0; если то импульсное управление оптимально.

в) Наконец, пусть - точка супердифференцируемости функции W(y), и - суперградиент. Тогда можно судить о неоптимальности импульсного и постоянного управлений (соответственно, при и )

Более детально связь между решением уравнения Гамильтона-Якоби (4.9) и оптимальностью данного конкретного управления рассматривается в работе [9].

Присутствие бесконечности в уравнении (4.8) объясняется скачками управления: мгновенное изменение влечет бесконечную производную по времени.