2. Функция цены

Пусть функция , называемая в дальнейшем функцией цены, определяется равенством

Теорема 2.1. Если выполнены условия (А) и (Б), то функция V непрерывна по совокупности переменных . Кроме того, справедливы следующие оценки:

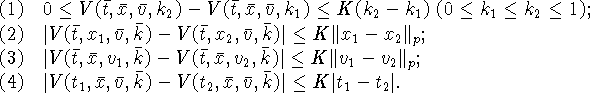
Доказательство. Зафиксируем и точку . Для любого по определению функции цены существует такое допустимое управление что

Далее будем для удобства считать функцию v(t) непрерывной справа на . Будем также полагать, что . Доказательство оценки в общем случае отличается несущественно.

Определим точку следующим образом:

Положим

Очевидно, . Пусть - траектория, выпущенная в момент из точки и соответствующая управлению Заметим, что если то эти траектории совпадают. Пусть . На интервале траектории также совпадают. Предположим, тогда из условия (А) следует, что

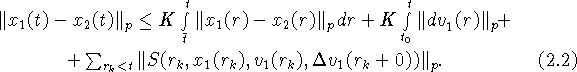
Оценим второе слагаемое в правой части (2.2):



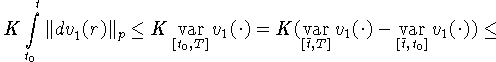
В третьем слагаемом неравенства (2.2), под знаком нормы, добавим и вычтем функцию скачков специального вида:





Согласно [3, с. 164,], для первой из сумм в правой части неравенства (2.3) справедлива оценка





поскольку функции и , как отмечалось выше, равномерно ограничены.

Применяя определение (1.5) функции скачков ко второй сумме в правой части (2.3), получаем

Таким образом,

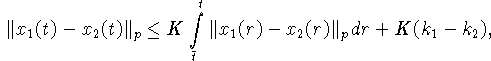
откуда, пользуясь леммой Гронуолла, имеем

Данная оценка позволяет установить, что



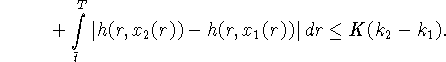
Следовательно, из (2.1) имеем



В силу произвольности ,

Осталось доказать, что эта разность неотрицательна. Для любого существует такое, что Пусть тогда т.е., управление - допустимое. Далее, так как то

и результат следует из произвольности

Проверка непрерывности V по и не представляет сложности.

Докажем непрерывную зависимость V от . Зафиксируем и точку Для любого подберем управление так, чтобы

Положим

если (случай рассмотрим отдельно). Тогда Пусть - траектория, выпущенная в момент из точки и соответствующая управлению Тогда условие (А), тождества оценка (2.4) и лемма Гронуолла приводят к неравенству (при )

следовательно,

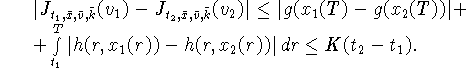
Таким образом,

В силу произвольности можно заключить, что

При положим на отрезке . Проводя аналогичные рассуждения, получим

Объединяя (2.5) и (2.6), получаем, что для любых справедливо неравенство

В завершение доказательства Теоремы 2.1 сформулируем следующее

Предложение 2.1. Функция цены удовлетворяет краевому условию

где и граничному условию

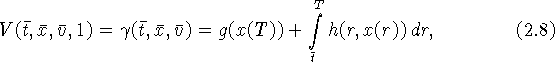
где x(t) - решение задачи Коши

Доказательство. Равенство (2.8) следует немедленно из непрерывности функции цены по переменной k, а также из того, что при k=1 весь ресурс исчерпан, и единственным допустимым управлением будет для всех

Проверим краевое условие (2.7). Зафиксируем и Пусть определим управление следующим образом: . Пусть - траектория, выпущенная в момент из точки и соответствующая управлению ; тогда

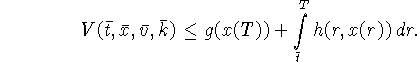
Если , то

Обратно, пусть - произвольное. Тогда из условия (Б) мы имеем, что







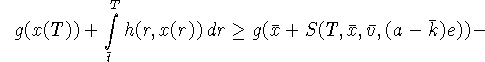
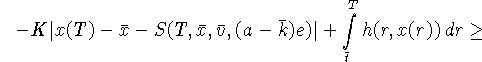
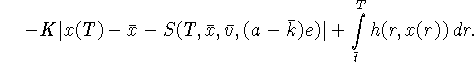
Пусть ; так как v - произвольное, то Сравнивая два полученных неравенства, мы видим, что имеет место равенство (2.7).