5. Пример

Рассмотрим следующую задачу оптимального управления. Пусть и движение объекта управления описывается дифференциальным уравнением



При множество допустимых управлений -

Нетрудно проверить, что для уравнения (5.1) условие (А) выполнено.

Траектория отвечающая допустимому управлению имеет вид:

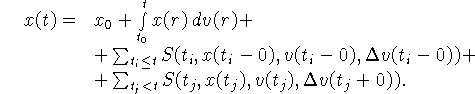
Остановимся на функции скачков: согласно (1.5),

где

Таким образом,

т.е. момент подачи импульса и пре-ущее значение управления на величину скачка не влияют.

Пусть минимизируемый функционал представляет собой расстояние до нуля в конечный момент:

Условие (Б) для нашей задачи выполнено.

Функция цены

должна удовлетворять следующим краевому и граничному условиям:

и

Рассмотрим подробно условие (5.3). Пусть где - параметр, Функция f(a) достигает экстремальных значений на концах отрезка [k,1]:



Минимальное из этих значений и есть правая часть (5.3):

Равенства (5.2), (5.4) и (5.5) подсказывают нам следующую оптимальную стратегию: в начальный (или любой другой) момент времени подаем импульс в остальное время управляющее воздействие не применяется. Пусть траектория отвечает выбранному управлению; положим

Покажем, что функция является функцией цены задачи, то есть есть вязкое решение на множестве уравнения Гамильтона-Якоби

Частные производные существуют и непрерывны во всей области частная производная не определена только в точках вида (t,0,v,k). Это точки субдифференцируемости функции субградиенты имеют вид где Таким образом, мы имеем:

Следовательно, - верхнее вязкое решение уравнения (5.6) в точках (t,0,v,k). Во всех остальных точках множества функция непрерывно дифференцируема, и







Подставляя эти значения в уравнение (5.6), получаем тождество, т.е.
- классическое решение на множестве

Замечание. Случай не укладывается в общую схему оптимального управления, поскольку

для всех

Поступила 08.09.97