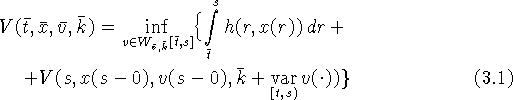
и
Предложение 3.1.
Пусть условия
(А) и (Б)
выполнены. Тогда для любого ![]() справедливо
справедливо
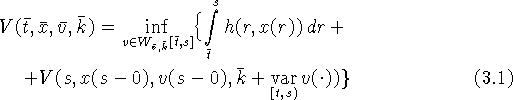
и
![]()
Доказательство. Остановимся на доказательстве равенства (3.2), так как (3.1) проверяется стандартным способом (см., например, [1]).
Пусть ![]() означает правую часть
(3.2). Поскольку
означает правую часть
(3.2). Поскольку ![]() можно взять равным нулю, мы
видим, что
можно взять равным нулю, мы
видим, что ![]()
С другой стороны, зафиксируем ![]() и пусть управление
и пусть управление ![]() будет следующим:
будет следующим:
![]() .
Пусть
.
Пусть ![]() - траектория, выпущенная в момент
- траектория, выпущенная в момент ![]() из точки
из точки ![]() и соответствующая управлению
и соответствующая управлению ![]() .
Тогда для любого
.
Тогда для любого ![]() при
при ![]() мы имеем из (3.1):
мы имеем из (3.1):
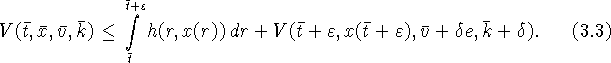
Устремляя ![]() к нулю, так как
к нулю, так как ![]() ,
можно заключить из (3.3)
и непрерывности V, что
,
можно заключить из (3.3)
и непрерывности V, что
![]()
для всех ![]() Следовательно,
Следовательно, ![]() что и требовалось доказать.
что и требовалось доказать.
Используя те же рассуждения, можно получить следующие результаты.
Лемма 3.1.
Отображение ![]() не убывает на интервале
не убывает на интервале ![]() .
.
Следствие 1.
Если в ![]() минимум достигается при
некотором
минимум достигается при
некотором
значении
![]() , то на
интервале
, то на
интервале ![]() отображение
отображение
![]() постоянно.
постоянно.
Следствие 2.
Можно объединить ![]() ,
,
![]() получая
получая
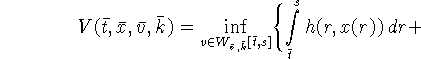
![]()
![]()