12. О гладкости решений

Прежде всего следует отметить, что для гладкости решений ФДУ необходима (но не достаточна !) соответствующая гладкость начальной функции.

Например, если мы хотим исследовать существование (k+1)-ой производной решения уравнения

то соответствующая начальная функция должна принадлежать классу . Поэтому всюду в дальнейшем будем предполагать, что начальная функция обладает необходимой гладкостью.

12.1. О гладкости решения в начальной точке. Как известно [18, 28], решения ФДУ могут иметь разрывы производной в начальной точке.

Для того, чтобы в начальный момент времени решение уравнения (1.1), соответствующее начальной функции , было непрерывно дифференцируемо необходимо и достаточно выполнения условия

называемого условием склейки 1-го порядка. Напомним, что включение означает, что функция , определенная на полуинтервале , может быть продолжена в классе на весь интервал , причем . Поэтому далее считаем .

Для непрерывности k-й производной решения в начальный момент времени необходимо и достаточно выполнения условия склейки k-го порядка

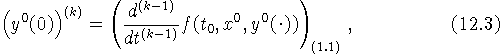
где - k-я правая производная начальной функции в нуле;
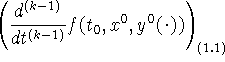- (k-1)-я полная производная функционала f в силу системы (1.1) в точке . При этом предполагается, что функционал f имеет в точке частные и инвариантные производные по t, x, до (k-1)-го порядка включительно.

Теорема 12.1. Для того, чтобы решение уравнения (1.1) имело в начальный момент времени двусторонние непрерывные производные до k-го порядка включительно, достаточно выполнения условий склейки до (k-1)-го порядка.

12.2. О гладкости решения на интервале.

Теорема 12.2. Если отображение имеет инвариантно непрерывные частные и инвариантные производные по t, x и до m-го порядка и выполняются условия склейки до m-го порядка, то всякое решение уравнения (1.1) имеет непрерывные производные по t до (m+1)-го порядка.

Доказательство. Пусть x(t), , - решение задачи (1.1) - (1.3). Тогда на отрезке имеет место тождество

Из непрерывности на отрезке функции x(t) и инвариантной непрерывности отображения f следует непрерывность функции x'(t) на .

Так как , то отображение имеет инвариантно непрерывные частные производные по t и x, а также инвариантную производную по , и, следовательно, правая часть (12.4) имеет непрерывную производную по t. Тогда функция x(t) имеет на непрерывную производную 2-го порядка. Продифференцировав (1.1) по t, получаем



Если , то, в силу существования инвариантно непрерывных производных второго порядка отображения , можно, дифференцируя еще раз тождество (1.1), доказать существование и непрерывность на третьей производной решения x(t).

Повторяя эти рассуждения m раз, докажем утверждение теоремы.

12.3. О плотности. При построении численных методов решения ФДУ требуется, как правило, достаточная гладкость решений. Однако, во многих случаях соответствующая гладкость будет иметь место только при выполнении условий склейки соответствующих порядков.

Если же условия склейки не выполены, то стараются, как правило, построить специальные алгоритмы в предполагаемых точках разрывов производных.

Цель данного пункта состоит в том, чтобы показать, что, как правило, при построении численных методов можно практически всегда предполагать выполненными условия склейки.

Рассмотрим для простоты уравнение с постоянным запаздыванием (12.1). Для непрерывной дифференцируемости решения в начальный момент времени необходимо и достаточно, чтобы начальная функция удовлетворяла условию склейки 1-го порядка

Условие склейки 2-го порядка имеет вид



Условие склейки 3-го порядка имеет вид

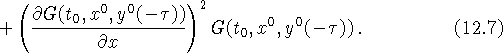
Рассмотрим некоторую начальную функцию не удовлетворяющую условиям склейки (12.5) - (12.7).

Так как правые части в условиях (12.5) - (12.7) не зависят от значений начальной функции на интервале (Для .), то, очевидно, функцию можно изменить на интервале таким образом, что для измененной функции соответствующая начальная пара будет обладать требуемой гладкостью и удовлетворять условиям склейки (требуемого порядка), причем норма может быть сделана сколь угодно малой.

Тогда мы можем считать, что решаем задачу для начальной функции , удовлетворяющей условиям склейки.

Учитывая, что при построении численных методов используются значения функции лишь в дискретные моменты времени, то считая меньше шага разбиения (сетки), можно предполагать, что начальная функция удовлетворяет условиям склейки.

Нетрудно показать, что в общем случае справедлива следующая

Теорема 12.3. Пусть функция в правой части системы (12.1) непрерывно дифференцируема до k-го порядка. Тогда множество функций из , удовлетворяющих условию склейки до k+1-го порядка, плотно в ( в норме пространства ).

Поступила 18.11.97