4. Доказательство теоремы

Для доказательства первого утверждения теоремы (сходимости (5)) достаточно проверить выполнение условий (13) - (15) леммы 2. Рассмотрим условие (13). Покажем, что функция 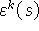удовлетворяет неравенству (13) и найдем L и 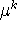. Воспользуемся равенством 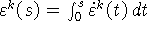. Возьмем произвольное 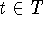. Напомним, что промежуток T разбивается с шагом 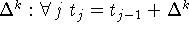, 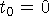. Считаем, что 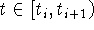. Запишем следующее отношение, причем 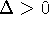выбираем так, чтобы :



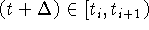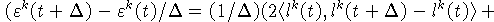
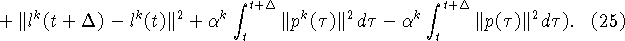
Оценим второе слагаемое в правой части (25):



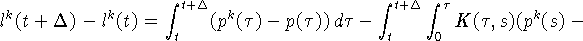
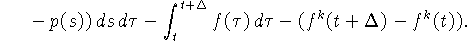
Имеем (см. (4), (9))

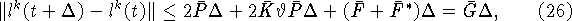
здесь 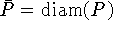, 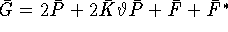. Тогда

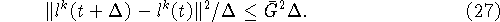
Запишем слагаемые, оставшиеся в правой части (25), в следующем виде





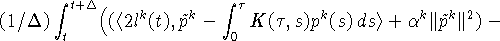
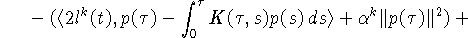
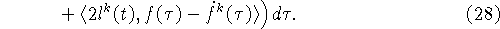
Из правила нахождения 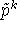следует



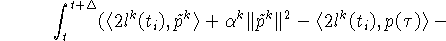
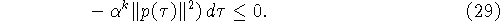
Отсюда выводим:







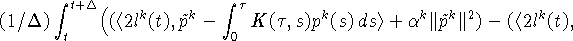
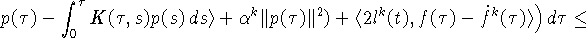
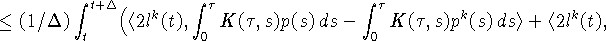
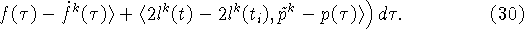
Из определения (3) следует оценка:

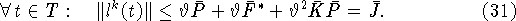
Используя (8) и (31), оцениваем интеграл от первого скалярного произведения в правой части (30):









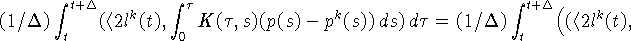
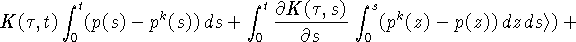
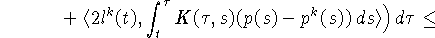
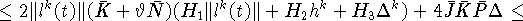
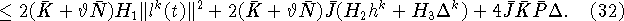
Принимая во внимание (9), (11), (26), (31) и используя теорему Фубини, получаем следующую оценку для второго скалярного произведения в правой части (30) :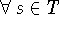















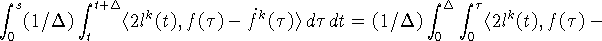
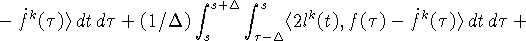
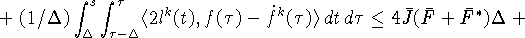
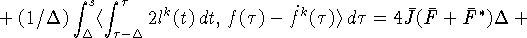
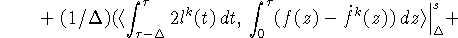
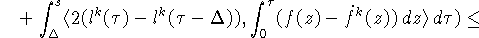
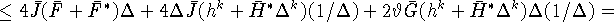
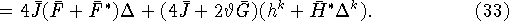
Учитывая (26), оцениваем интеграл от третьего скалярного произведения в правой части (30):

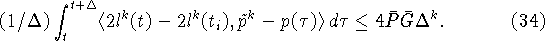
Объединяя (27), (32) - (34), переходя к пределу при 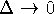в отношении (25) и интегрируя по промежутку [0, s], получаем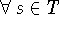









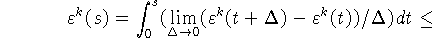
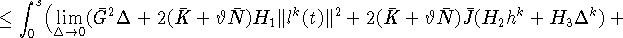
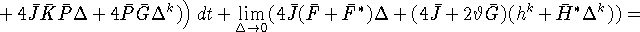
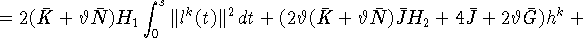
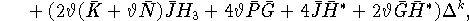
откуда

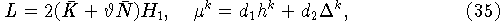
где , .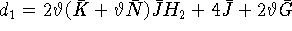

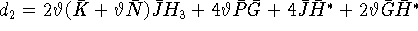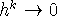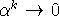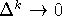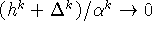По условию теоремы , , и при 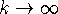. Поэтому выполняется условие (14) леммы 2. Условие (15) также справедливо, поскольку

а) имеет место сходимость интегралов:

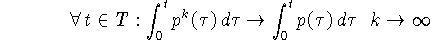
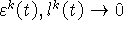( при 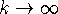, и выполняется оценка (8));

б) .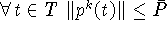

Сходимость (5) доказана. Покажем, что выполняется оценка (6). Запишем следующее неравенство (см. (20) - (22)):

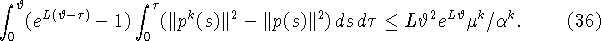
Поскольку



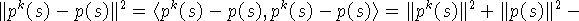
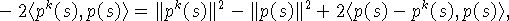
то





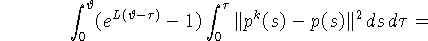
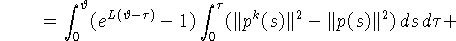
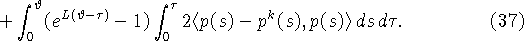
Справедлива следующая оценка [4]:



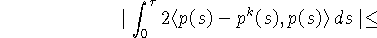
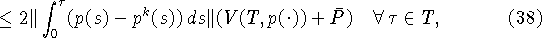
здесь 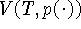- вариация функции 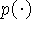на промежутке T.

По утверждению леммы 1:

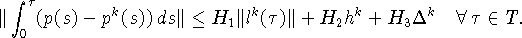
Кроме того, из (12) и (13) следует



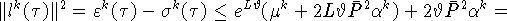
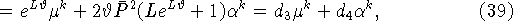
где 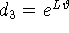, 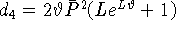. Тогда 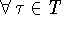выполняется

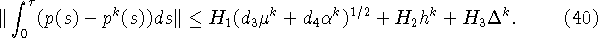
Объединяя (36) - (40), получаем



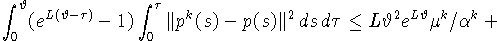
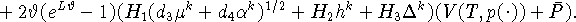
С другой стороны,







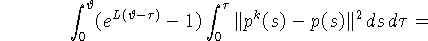
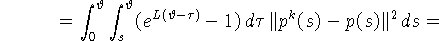
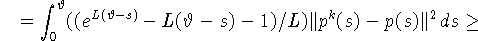
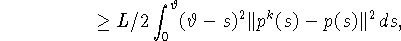
откуда

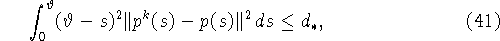
где



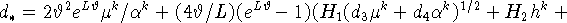
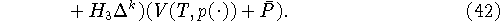
Полагая

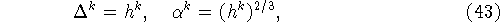
получаем из (41) и (42) первую оценку (6).

Кроме того, из (41) следует

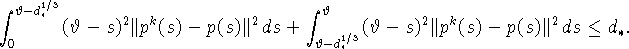
Так как

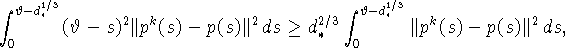
то

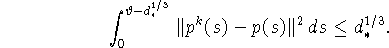
Добавляя к полученному очевидное неравенство

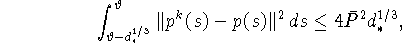
имеем оценку

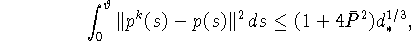
из которой, учитывая определения 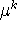и 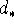(см. (35) и (42)), получаем оценку





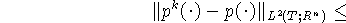
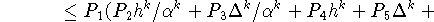
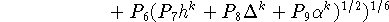
при следующих значениях входящих в неравенство констант:





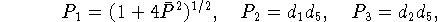
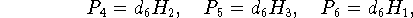
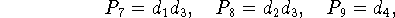
где константы 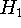, , 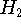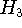были введены в лемме 1, 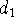, 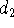- в формуле (35), 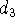, 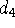- в формуле (39), 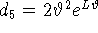, 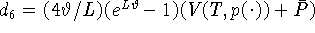. Отсюда находим константу 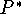и, таким образом, показываем справедливость второй оценки (6). Теорема 1 доказана.

З а м е ч а н и е. Легко видеть, что для получения порядка по h второй оценки (6) следует потребовать выполнения соотношений (43). В этом случае имеем

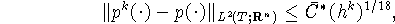
константа 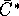может быть выписана явно.

Рассмотрим задачу, аналогичную сформулированной в первом пункте, в предположении, что измеряется не интеграл от правой части уравнения (1), а сама функция 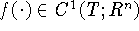, т.е. в дискретные, достаточно частые, моменты времени 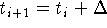, , 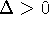, , 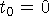, 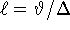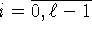поступает информация 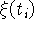, причем

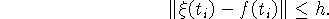
Приближенное решение 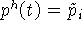, , 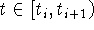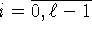находится посредством процедуры, аналогичной (3), (4): 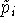есть решение экстремальной задачи



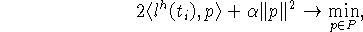
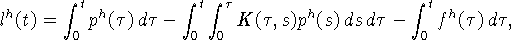
здесь 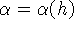, 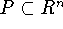и интерполянт 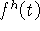имеют тот же смысл, что и в (3), (4). В предположении, что выполняется согласование параметров, введенное в теореме 1, справедлива

Теорема 2. Имеет место сходимость:

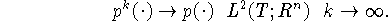
Если функция 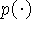имеет на промежутке T ограниченную вариацию, то справедливы следующие оценки скорости сходимости алгоритма:



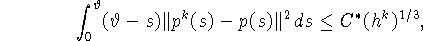
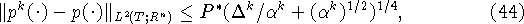
где константы 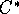и 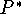могут быть выписаны явно.

Доказательство отличается от доказательства теоремы 1 лишь техническими деталями, поэтому его опустим.

З а м е ч а н и е. Легко видеть, что для получения порядка по h второй оценки (44) следует потребовать выполнения соотношений (43). В этом случае имеем

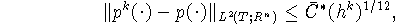
где константа 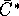может быть выписана явно.

Итак, в работе предложен алгоритм приближенного решения интегрального уравнения Вольтерра II рода. Он устойчив по отношению к информационным и вычислительным погрешностям, полученное согласование параметров конструктивно.