5. Численный пример

Рассматривалось интегральное уравнение следующего вида:

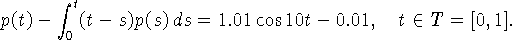
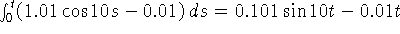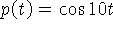Измерялся (с погрешностью h) интеграл от правой части, т. е. функция . Точное решение уравнения - функция . Было выбрано следующее согласование параметров алгоритма (см. формулировку теоремы 1):

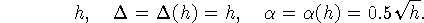
Результаты численных расчетов приведены на рисунках 1, 2.

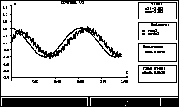
Рис. 1: (Монитор)

Значения параметров: h = 0.01, , .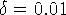

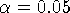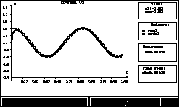
Рис. 2: (Монитор)

Значения параметров: h = 0.001, , .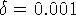

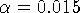Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, грант 96-01-00846.

Поступила 16.02.96

СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ

1. Апарцин А.С. Дискретизованные методы регуляризации некоторых интегральных уравнений I рода // Методы численного анализа и оптимизации.- Новосибирск. 1987.- С.263-297.
2. Бухгейм А.Л. Уравнения Вольтерра и обратные задачи. - Новосибирск. Наука. 1983.- 207 с.
3. Верлань А.Ф., Сизиков В.С. Методы решения интегральных уравнений. - Киев. Наукова думка. 1978.- 291 с.
4. Вдовин А.Ю. Оценки погрешности в задаче динамического восстановления управления // Задачи позиционного моделирования: Сб. ст. / АН СССР. УНЦ.- Свердловск: УНЦ АН СССР, 1986.- С.3-11.
5. Денисов А.М О приближенном решении уравнения Вольтерра I рода // Журнал вычислительной математики и математической физики.- 1975. - Т. 15.  2.- С.1053-1056.
6. Иванов В.К., Васин В.В., Танана В.П. Теория линейных некорректных задач и ее приложения.- М. Наука. 1978.- 206 с.
7. Красовский Н.Н Управление динамической системой. - М. Наука. 1985.- 199 с.
8. Кряжимский А.В., Осипов Ю.С. О моделировании управлений в динамической системе // Изв. АН СССР. Техн. кибернетика.- 1983.-  2.- С.51-60.
9. Осипов Ю.С., Кряжимский А.В. О динамическом решении операторных уравнений // Докл. АН СССР.- 1983.- Т.269.  3.- С.552-556.
10. Осипов Ю.С., Кряжимский А.В., Максимов В.И. Задачи динамической регуляризации для систем с распределенными параметрами // Препринт ИММ УрО АН СССР.- 1991.
11. Розенберг В.Л. О восстановлении функции источника в параболическом уравнении // Тезисы докл. Второго Международного семинара ``Негладкие и разрывные задачи управления и оптимизации''.- Челябинск. - 1993.- С.119-120.
12. Розенберг В.Л. Задача динамического восстановления функции источника в параболическом уравнении // Труды ИММ УрО РАН.- 1995. - Выпуск III.- С.116-135.
13. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. - М. Наука. 1978.- 285 с.
14. Трикоми Ф. Интегральные уравнения.- М. Изд. иностр. литер. 1960.- 299 с.
15. Kryazhimskii A.V., Maksimov V.I., Samarskaya E.A. Input reconstructibility of parabolic systems // IIASA, Laxenburg, Austria.- WP-95-17.- 1995.
16. Maksimov V.I., Rozenberg V.L. Feedback approximation of a control under the conditions of uncertainty.- The Third International Workshop ``Multiple criteria problems under uncertainty''.- Orekhovo-Zuevo. Russia.- September 5-9. 1994.- P.54.
17. Osipov Yu.S., Kryazhimskii A.V. Inverse problems for ordinary differential equations: dynamical solutions.- Gordon & Breach.- 1995.