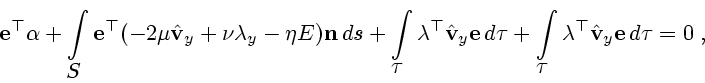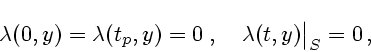5. Оптимизация обтекания: общий случай

При ограничениях L1-L3 рассматриваются поступательные перемещения твердого тела по заданной траектории. При этом положение тела в начальный и конечный момент времени считается заданным. Наша цель - определить, как должно двигаться тело, чтобы минимизировать энергетические затраты на преодоление сопротивления жидкости? Если в качестве управления считать приложенную к телу силу, то задача принадлежит к числу сингулярных (или нерегулярных) и, вообще говоря, осложнена формальной необходимостью перемножения импульсной составляющей в давлении на одновременно терпящую разрыв скорость перемещения тела.

Задача может быть редуцирована к несингулярной задаче динамической оптимизации по следующей схеме. В начальный момент центр инерции тела находится в начале системы координат $O x_1 x_2 x_3$. Уравнения движения имеют вид

$$\dot {\bf x}_c=u(t)\,{\bf e}(t)\;,\quad {\bf x}_c(0)=0\,,$$ (5.1)

где ${\bf e}(t)$ - заданная вектор-функция. Вспомогательная задача состоит в определении программы $u^o(t)$, соответствующей наименьшим затратам энергии на преодоление силы сопротивления жидкости. Такая задача уже не является сингулярной. В предположении, что поверхность тела $S$ является замкнутой и регулярной [24], главный вектор сил воздействия жидкости на тело можно рассчитать по формуле (2.5), в которой ${\bf v}(t,x)={\bf v}(x_c(t)+y)=\hat {\bf v}(t,y)$. Вектор $\hat {\bf v}$ является вектором абсолютной скорости движения жидкости, отнесенным к подвижной системе $Oy_1y_2y_3$, жестко связанной с телом.

Теперь можно подсчитать мощность:

$$\dot A=u{\bf e}^\top(-{\bf R})\;,\quad A(0)=0\,.$$ (5.2)

Анализ уравнения Навье-Стокса (2.6) с учетом условия прилипания
${\bf v}(t,y)\bigl.\bigr\vert _S=u(t)\,{\bf e}(t)$ показывает, что формальное применение разрывных управлений приводит к появлению в правой части (6.2) произведения импульсной по времени компоненты давления на одновременно терпящую разрыв скорость движения тела. Это затруднение может быть преодолено при помощи следующего утверждения.

Лемма 5.1. Пусть $\hat p(t,y)$, $\hat {\bf v}(t,y)$ и $\partial\hat {\bf v}(t,y)/\partial y$ исчезают при $y\to\infty$. Тогда работа допускает представление

$$A=a+\frac{\rho}{2}\int\limits_{{\displaystyle \tau}}\hat {\bf v}^\top \hat {\bf v}\,d\tau\,,$$ (5.3)

$$\dot a=\mu\int\limits_{{\displaystyle \tau}}\vert\vert\hat {... ... \tau}} \hat {\bf v}^\top (0+0,y)\hat {\bf v}(0+0,y)\,d\tau\,,$$ (5.4)

где $\tau$ - дополнение тела до всего пространства.

Для обоснования леммы следует учесть в правой части (6.2) условие прилипания, воспользоваться формулой Остроградского, выражением для $\partial\hat p/\partial y$, вытекающим из уравнения Навье-Стокса (2.6) с ${\bf V}=u(t)\,{\bf e}(t)$, и затем снова формулой Остроградского. При этом произведение ${\bf v}^\top D_t {\bf v}$ считать равным $\frac{1}{2}\,D_t(\hat {\bf v}^\top\hat {\bf v})$ [13], где $D_t$ - оператор обобщенного дифференцирования.

Поскольку не исключается наличие в давлении импульсных составляющих, то его следует искать в виде обобщенной производной обычной функции $q(t,y)$. Тогда уравнение Навье-Стокса (2.6) преобразуется к следующей системе:

$$\begin{array}{l} p=D_t q\;,\\ {\bf U}_t=-\hat {\bf v}_y(\hat... ...;,\quad \hat {\bf v}={\bf U}-\frac{1}{\rho}\,q_y\;. \end{array}$$ (5.5)

Итак, исходная задача редуцирована к задаче минимизации (6.3) в момент $t_p$ при динамических ограничених (6.5), $\mathop{\rm div}\nolimits \hat {\bf v}=0$, начальном условии $\hat {\bf v}(0,y)=0$, условии прилипания и указанных в лемме 5.1 условиях на бесконечности. Теперь к этой задаче можно применить классическую процедуру Лагранжа и получить следующее утверждение.

Теорема 5.1. Имеют место следующие необходимые условия оптимальности

$$\hat {\bf v}(t_p,y)=0\;,$$

$${\bf e}^\top\alpha+\int\limits_{{\displaystyle S}}{\bf e}^\to... ...playstyle \tau}}\lambda^\top \hat {\bf v}_y{\bf e}\,d\tau=0\;,$$

$$\lambda_t=\hat {\bf v}_y^\top\lambda-\lambda_y(\hat {\bf v}-... ...mathop{\rm div}\nolimits (2\mu \hat {\bf v}_y-\nu\lambda_y)\;,$$

$$\mathop{\rm div}\nolimits \lambda_t=0\;,$$

$$\lambda(0,y)=\lambda(t_p,y)=0\;,\quad \lambda(t,y)\bigl.\bigr\vert _S=0\,,$$

где $\alpha$, $\eta$, $\lambda$, - множители Лагранжа.