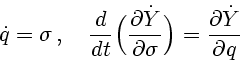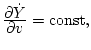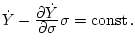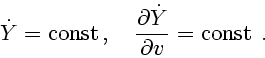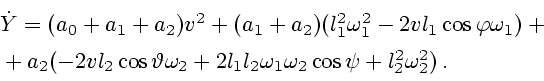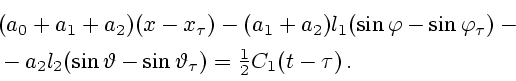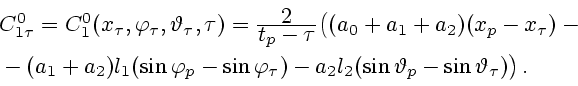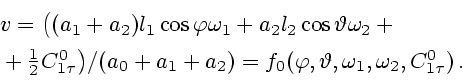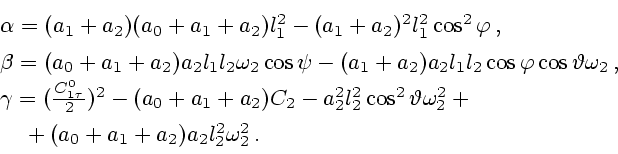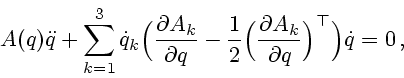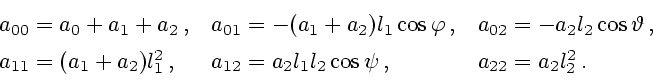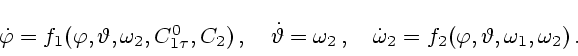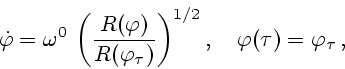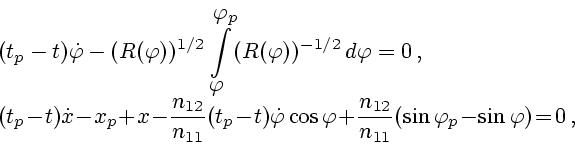

Next: 7 Вопросы обоснования: уравнения
Up: ZAV
Previous: 5 Оптимизация обтекания: общий
В [15,29,30] представлены модели однозвенного, двухзвенного и многозвенного
транспортных манипуляторов (ТМ) для перемещения грузов в жидкости (см. рис. 3).
Считается, что ТМ состоят из последовательно соединенных при помощи цилиндрических
шарниров осесимметрических звеньев. Шарниры располагаются в центрах масс звеньев, и
их оси параллельны друг другу, оси звеньев находятся в одной плоскости, называемой
плоскостью ТМ. Однозвенный транспортный манипулятор (ОТМ) статически уравновешен (за счет
изменяемой длины его выдвижной части) и его часть - противовес
- находится в корпусе носителя. Предполагается, что в шарнирах
ТМ действуют создаваемые внутренними усилиями управляющие моменты так, что действующий на
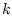 -е звено момент
-е звено момент 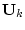 сопровождается действующим на
сопровождается действующим на 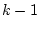 -е звено моментом
-е звено моментом
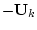 ,
, 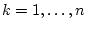 . Движение носителя ТМ осуществляется при помощи действующей
в его плоскости горизонтальной силы
. Движение носителя ТМ осуществляется при помощи действующей
в его плоскости горизонтальной силы 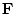 . Рассматриваемая механическая система
находится в жидкости. Поэтому помимо управляющих воздействий и сил тяжести
. Рассматриваемая механическая система
находится в жидкости. Поэтому помимо управляющих воздействий и сил тяжести 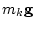 (
(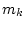 - масса
- масса 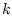 -го звена) на звенья действуют также силы Архимеда и
гидродинамические силы. Последние могут быть приведены к силам
-го звена) на звенья действуют также силы Архимеда и
гидродинамические силы. Последние могут быть приведены к силам
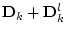 ,
приложенным к центрам масс звеньев, и моментам
,
приложенным к центрам масс звеньев, и моментам 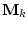 . При этом силы лобового
сопротивления
. При этом силы лобового
сопротивления 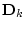 и подъемные силы
и подъемные силы 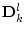 действуют в плоскости ТМ, а
моменты
действуют в плоскости ТМ, а
моменты 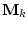 ей перпендикулярны. Эти моменты обусловлены несовпадением в общем
случае центров давления гидродинамических сил с центрами масс звеньев. На основе
описанной физической модели ТМ можно рассматривать эквивалентные плоские механические
системы точечных масс, последовательно соединенных бесконечно тонкими абсолютно жесткими
стержнями. Перечисленные выше силы приложены к этим точечным массам. Дифференциальные
уравнения движения ТМ получены в форме уравнений Лагранжа 2-го рода для эквивалентных
систем точечных масс (см. раздел 7). Литература по робототехнике содержит достаточно
полное описание приводов различного типа, создающих угловые управляющие моменты. В работе
рассмотрены два типа приводов. Первый из них реализует угловой момент
ей перпендикулярны. Эти моменты обусловлены несовпадением в общем
случае центров давления гидродинамических сил с центрами масс звеньев. На основе
описанной физической модели ТМ можно рассматривать эквивалентные плоские механические
системы точечных масс, последовательно соединенных бесконечно тонкими абсолютно жесткими
стержнями. Перечисленные выше силы приложены к этим точечным массам. Дифференциальные
уравнения движения ТМ получены в форме уравнений Лагранжа 2-го рода для эквивалентных
систем точечных масс (см. раздел 7). Литература по робототехнике содержит достаточно
полное описание приводов различного типа, создающих угловые управляющие моменты. В работе
рассмотрены два типа приводов. Первый из них реализует угловой момент 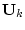 ,
имеющий природу момента, создаваемого парой сил. Этому, например, соответствует случай,
когда момент
,
имеющий природу момента, создаваемого парой сил. Этому, например, соответствует случай,
когда момент 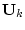 создается электродвигателем со статором на одном звене и
ротором, жестко связанным с соседним звеном. Во втором случае угловой момент
создается электродвигателем со статором на одном звене и
ротором, жестко связанным с соседним звеном. Во втором случае угловой момент 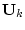 создается посредством выходного штока переменной длины с фиксированным шарнирным
закреплением на предыдущем звене. Для ОТМ установлено, что форма обобщенной силы
создается посредством выходного штока переменной длины с фиксированным шарнирным
закреплением на предыдущем звене. Для ОТМ установлено, что форма обобщенной силы
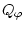 (
(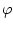 - угловая координата манипулятора) является инвариантной по
отношению к способу реализации углового момента манипулятора.
- угловая координата манипулятора) является инвариантной по
отношению к способу реализации углового момента манипулятора.
Рис. 3. Многозвенный транспортный манипулятор.
Таким образом, в [29] указаны формулы для составляющих обобщенных сил,
соответствующих действующим на звенья ТМ силам лобового сопротивления и подъемным
силам. Установлена инвариантность формы обобщенных сил, соответствующих обобщенным
угловым координатам, по отношению к способам реализации приложенных к звеньям ТМ
управляющих моментов.
Во введении были перечислены три особенности рассматриваемых задач энергетической
оптимизации. Третья из них состоит в проблеме подсчета энергетических затрат. Формально
для ее решения надо определить корректный с точки зрения теории обобщенных функций способ
умножения разрывных обобщенных скоростей на импульсные управляющие воздействия
(см. раздел 7). Однако в [29] выбран другой подход. Именно с использованием схем,
описанных в [10,13], исходные задачи редуцируются к вспомогательным
классическим задачам динамической оптимизации. Такой подход соответствует строгой
математической формализации указанных нелинейных операций над обобщенными функциями
(см. раздел 7). Редукция опирается на то, что движение ТМ происходит в потенциальном поле
силы тяжести, и при этом часть работы расходуется на изменение кинетической энергии ТМ.
Поскольку граничные условия заданы, варьируемая часть работы
- это энергетические затраты на преодоление сил сопротивления. Вычисление мощности,
соответствующей этим затратам, приводит к вспомогательной задаче минимизации таких затрат
при ограничениях в виде кинематических связей ТМ и уравнения для энергетических затрат на
преодоление сил сопротивления. Так построенная вспомогательная задача по форме
принадлежит к числу задач классического вариационного исчисления. Так оно и есть в тех
случаях, когда ТМ состоит из тел с гладкой поверхностью. Если в состав ТМ входят тела с
кусочно-гладкой поверхностью (например, цилиндрические тела), то в пространстве
обобщенных координат и скоростей исходной задачи появляются многообразия, на которых
проекция этих тел на плоскость, перпендикулярную вектору скорости их центра масс, а
следовательно, и гамильтониан теряют свойство дифференцируемости.
Общий итог проведенных исследований можно сформулировать так. На оптимальном перемещении
ТМ мощность сохраняет постоянное значение. Если в точках оптимальной фазовой траектории
мощность дифференцируема по обобщенным скоростям звеньев ТМ, то ее частная производная
по скорости носителя остается постоянной.
Более подробно, вводятся следующие обобщенные координаты многозвенного транспортного
манипулятора (МТМ): 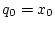 - смещение носителя по горизонтали,
- смещение носителя по горизонтали, 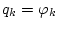 ,
,
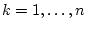 - угол между вертикалью и
- угол между вертикалью и 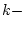 ым звеном. Тогда выражение для мощности
гидродинамических сил имеет вид
ым звеном. Тогда выражение для мощности
гидродинамических сил имеет вид
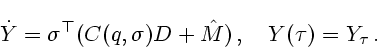 |
(6.1) |
Здесь
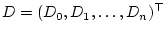 ,
, 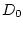 ,
, 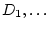 ,
, 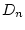 - величины сил лобового
сопротивления, приложенных к центрам инерции звеньев
- величины сил лобового
сопротивления, приложенных к центрам инерции звеньев 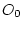 ,
, 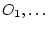 ,
, 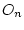 соответственно,
соответственно,
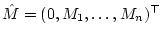 ,
, 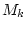 - момент действующих на
- момент действующих на 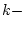 е
звено гидродинамических сил,
е
звено гидродинамических сил, 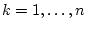 ,
, 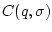 -
-
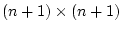 -матрица (см. раздел 7),
-матрица (см. раздел 7),
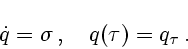 |
(6.2) |
Задача 6.1. Решить задачу минимизации 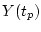 при динамических связях
(7.1), (7.2) и краевых условиях
при динамических связях
(7.1), (7.2) и краевых условиях 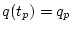 .
.
Пусть звенья МТМ имеют гладкую поверхность.
Задача 6.2. Найти начальные скорости
реализующие для системы
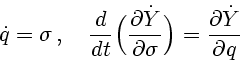 |
(6.3) |
граничные условия 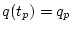 .
.
Стандартная процедура Эйлера-Лагранжа приводит к утверждению.
Теорема 6.1. Пусть выполнены ограничения L1-L3 и гипотеза 1.
Тогда
- -
- задача 6.1 и граничная задача 6.2 равносильны;
- -
- на промежутке
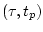 оптимальная фазовая
траектория МТМ
оптимальная фазовая
траектория МТМ
принадлежит многообразию, описываемому уравнением
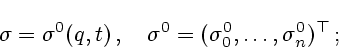 |
(6.4) |
- -
- на многообразии (7.4) выполняются соотношения
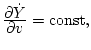
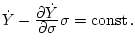
Замечание. Многообразия типа (7.4) согласно принятой терминологии
называют сингулярными [8,9].
В предположении гипотезы 2 согласно теореме Эйлера об однородных функциях третье
утверждение теоремы 6.1 имеет вид
Итак, установлено, что программы оптимальных переходов имеют
двухимпульсную структуру.
Цель начального импульсного воздействия - сбросить фазовое изображение МТМ на особое
многообразие, вдоль которого движение происходит до тех пор, пока не будет достигнуто
состояние, из которого конечный импульс переводит МТМ в заданное положение. В результате
исходная задача сведена к граничной задаче. Такая задача решается численно обычно так
называемым методом стрельбы [14].
В условиях неопределенных флуктуаций жидкости управляющие воздействия входят в уравнения
движения МТМ с аддитивными помехами. Возникает задача о построении позиционного алгоритма
управления МТМ, который обладал бы свойством: в случае исчезновения возмущений алгоритм
обеспечивает оптимальное по отношению к сложившейся позиции завершение процесса
управления. В качестве такого алгоритма в работе используется позиционная процедура
импульсной коррекции, в результате которой осуществляется сброс фазового изображения МТМ
на особую поверхность (7.4). С уменьшением времени между последовательными
коррекциями фазовая точка все чаще начинает попадать на многообразие (7.4). В
результате в процесс управляемого движения МТМ вносится эффект типа скольжения вдоль
особой поверхности. Один из естественно возникающих здесь вопросов следующий:
будет ли с увеличением частоты коррекции фазовая
траектория МТМ стремиться к траектории, соответствующей [17] так называемому
идеальному скольжению? Такое скольжение описывается исходной возмущенной системой с
управлением, превращающим многообразие (7.4) в интегральное. Так как эта система
совпадает с системой оптимальных движений (7.2), (7.3), то положительный
ответ на поставленный вопрос позволил бы сделать вывод о том, что процедура импульсной
коррекции с неограниченно возрастающей частотой обеспечивает оптимальное поведение МТМ
при любых возмущениях 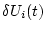
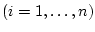 ,
, 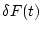 ,
, 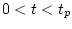 , и, в
частности, она решает задачу синтеза. Так оно и есть, поскольку уравнения движения МТМ и
особая поверхность (7.4) удовлетворяют условиям теоремы 2.2 [17].
, и, в
частности, она решает задачу синтеза. Так оно и есть, поскольку уравнения движения МТМ и
особая поверхность (7.4) удовлетворяют условиям теоремы 2.2 [17].
Ниже граничная задача, к которой сведено решение исходной задачи энергетической
оптимизации, описана более подробно для мобильных двухзвенных манипуляторов [30].
Рассмотрение ведется в рамках подхода Стокса.
В этом случае силы сопротивления жидкости звеньев прямо пропорциональны скоростям
перемещения их центров инерции, т.е. существуют 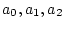 такие, что
такие, что
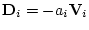 ,
, 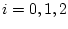 . Отсюда выражение для мощности сил лобового
сопротивления (7.1) будет иметь вид
. Отсюда выражение для мощности сил лобового
сопротивления (7.1) будет иметь вид
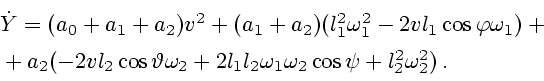 |
(6.5) |
С учетом этого для интеграла
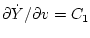 получается формула
получается формула
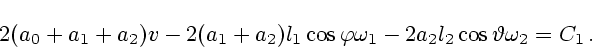 |
(6.6) |
Интегрирование (7.6) по промежутку 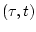 , приводит к соотношению
, приводит к соотношению
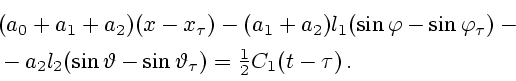 |
(6.7) |
Подстановка в (7.7) 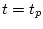 и граничных значений дает константу
и граничных значений дает константу 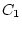 ,
соответствующую оптимальной траектории:
,
соответствующую оптимальной траектории:
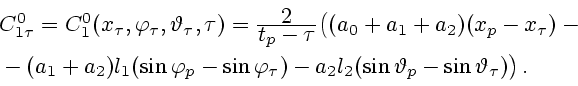 |
(6.8) |
В результате получено точное выражение смещения носителя двухзвенного ТМ в функции
текущего времени и угловых координат его звеньев, задаваемое формулами (7.7),
(7.8).
Формула (7.8) позволяет при помощи (7.6) вывести выражение для скорости
носителя:
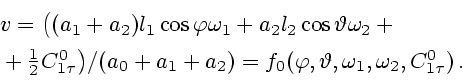 |
(6.9) |
Соотношение (7.9) дает возможность исключить из (7.5) линейную скорость
носителя ТМ и записать интеграл 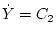 в виде
в виде
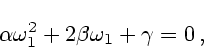 |
(6.10) |
где
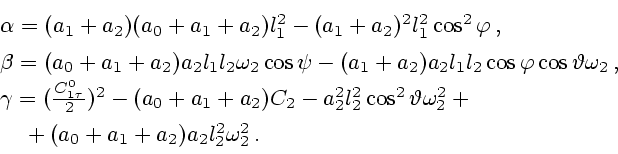 |
(6.11) |
Из (7.10) и (7.11) можно получить выражение для 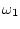 вида
вида
.
Подстановка выражения (7.5) во второе из уравнений (7.3) приводит к линейной
по ускорениям системе
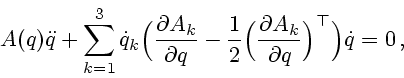 |
(6.12) |
где 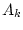 -
- 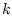 -й столбец симметричной матрицы
-й столбец симметричной матрицы 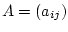 c элементами
c элементами
Из (7.12) можно получить выражение
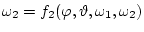 .
.
Таким образом, получена следующая система оптимальных движений
Для решения задачи 6.2 необходимо выбрать начальные значения скоростей
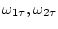 и константу
и константу 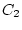 так, чтобы фазовое изображение ТМ
оказалось в последний момент
так, чтобы фазовое изображение ТМ
оказалось в последний момент 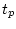 в заданном состоянии.
в заданном состоянии.
Задача об оптимальном перемещении однозвенного транспортного [15] манипулятора
формулируется и исследуется аналогично. Поэтому можно ограничиться указанием лишь
дополнительных фактов, обусловленных небольшой размерностью фазового пространства, равной
четырем, и тому, что рассмотрение ведется для случая малых чисел Рейнольдса, т.е. в
приближении Стокса. Система дифференциальных уравнений, описывающая оптимальное движение
ОТМ в промежуточные моменты процесса управления, допускает три интеграла. Эти интегралы
позволяют вычислить начальные условия и выписать непрерывные составляющие оптимальных
управлений в функции текущего значения угла поворота манипулятора 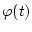 . Сама же
программа оптимального изменения угла
. Сама же
программа оптимального изменения угла 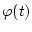 - решение
задачи Коши
- решение
задачи Коши
где
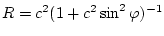 ,
, 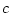 - константа, зависящая только от
геометрических характеристик ОТМ. Для ее решения можно воспользоваться таблицами для
эллиптических интегралов. Особая поверхность задается уравнениями
- константа, зависящая только от
геометрических характеристик ОТМ. Для ее решения можно воспользоваться таблицами для
эллиптических интегралов. Особая поверхность задается уравнениями
где приняты обозначения:
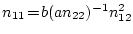 ,
,
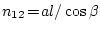 ,
,
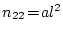 .
.


Next: 7 Вопросы обоснования: уравнения
Up: ZAV
Previous: 5 Оптимизация обтекания: общий
2003-06-25
![\includegraphics[height=0.35\textheight,width=0.7\textwidth]{c:/marinov/tom6rus/final2/zaval/MMM61.eps}](img335.gif)