![\includegraphics[%height=0.43\textheight,
width=0.7\textwidth]{c:/marinov/tom6rus/final2/zaval/cyl41.eps}](img195.gif)
Рис. 1. Транспортная система для перемещения мостовым краном
цилиндрического контейнера с грузом в бассейне с жидкостью.
В этом разделе приведена модель мобильной системы, предназначенной для перемещения при
помощи мостового крана цилиндрического контейнера с грузом в бассейне, заполненном вязкой
жидкостью (см. рис. 1). Система такого типа применяется для перемещения
цилиндрических чехлов с отработанными тепловыделяющими сборками в бассейнах выдержки
некоторых атомных электростанций. На основе этой модели поставлена задача об оптимальных
по расходу энергии перемещениях цилиндрического тела в вязкой жидкости при заданных
времени и дальности перемещения [28].
![\includegraphics[%height=0.43\textheight,
width=0.7\textwidth]{c:/marinov/tom6rus/final2/zaval/cyl41.eps}](img195.gif)
Положение системы описывается обобщенными координатами ![]() ,
, ![]() . Пусть
. Пусть ![]() -
линейная скорость точки захвата, а
-
линейная скорость точки захвата, а ![]() - угловая скорость цилиндра.
- угловая скорость цилиндра.
Движение крана осуществляется при помощи управляющей силы ![]() , линия действия которой
описывается уравнением
, линия действия которой
описывается уравнением ![]() . Из всех остальных действующих на кран сил ниже
учитывается только сила тяжести. На цилиндрический контейнер действует управляющий момент
. Из всех остальных действующих на кран сил ниже
учитывается только сила тяжести. На цилиндрический контейнер действует управляющий момент
![]() , сила тяжести, сила Архимеда и гидродинамическая сила. Работа, совершаемая
управляющими воздействиями
, сила тяжести, сила Архимеда и гидродинамическая сила. Работа, совершаемая
управляющими воздействиями ![]() и
и ![]() , описывается дифференциальным уравнением
, описывается дифференциальным уравнением
Задача 4.1. Требуется найти управляющие воздействия ![]() и
и
![]()
![]() переводящие с наименьшими затратами энергии
переводящие с наименьшими затратами энергии ![]() цилиндр
за заданное время
цилиндр
за заданное время ![]() на заданное расстояние
на заданное расстояние ![]() . В начальный и конечный моменты
цилиндр имеет вертикальную ориентацию.
. В начальный и конечный моменты
цилиндр имеет вертикальную ориентацию.
Ниже в краткой форме описано решение этой задачи с учетом только энергетических затрат на преодоление силы лобового сопротивления. Полное изложение результатов дано в статье [28].
Рассматриваемая задача является сингулярной и не может быть непосредственно решена при помощи классического вариационного исчисления. Ниже излагается редукция задачи 4.1 к вспомогательной задаче. Последняя не является сингулярной, однако принадлежит к числу задач негладкой оптимизации [26] и требует для своего решения специального подхода. Редукция опирается на то, что, во-первых, движение цилиндра происходит в потенциальном поле силы тяжести. Во-вторых, часть работы расходуется на изменение кинетической энергии цилиндра. Поэтому, поскольку граничные условия заданы, то варируемая часть работы, зависящая от выбора управляющих воздействий, - это энергетические затраты на преодоление силы лобового сопротивления.
В рамках гидродинамических ограничений L1-L3 и гипотезы 1 на движущийся в жидкости
цилиндр действуют сила лобового сопротивления и подъемная сила (2.9)-(2.11),
где ![]() - площадь проекции цилиндра на плоскость, перпендикулярную вектору его скорости
- площадь проекции цилиндра на плоскость, перпендикулярную вектору его скорости
![]() . Площадь
. Площадь ![]() однозначно характеризуется углом атаки цилиндра
однозначно характеризуется углом атаки цилиндра ![]() , т.е.
наименьшим по абсолютной величине углом между вектором
, т.е.
наименьшим по абсолютной величине углом между вектором ![]() и осью цилиндра (при
этом направление отсчета по часовой стрелки считается положительным, поскольку движение
цилиндра описывается в левой системе координат). Расчет площади
и осью цилиндра (при
этом направление отсчета по часовой стрелки считается положительным, поскольку движение
цилиндра описывается в левой системе координат). Расчет площади ![]() приводит к формуле
(
приводит к формуле
(![]() ,
, ![]() )
)
С учетом (5.1) выражение для мощности имеет вид
Направление оси цилиндра определяется вектором
Задача 4.2. Требуется найти функции ![]() ,
, ![]() , минимизирующие
терминальный функционал
, минимизирующие
терминальный функционал ![]() при динамических ограничениях
при динамических ограничениях
Задача имеет две особенности. Во-первых, оптимальный процесс обладает свойством симметрии
относительно момента времени ![]() . Поэтому достаточно найти экстремальные управления
для некоторых граничных условий
. Поэтому достаточно найти экстремальные управления
для некоторых граничных условий
![]() при свободной ориентации
цилиндра в момент времени
при свободной ориентации
цилиндра в момент времени ![]() Во-вторых, в силу отсутствия ограничений на величину
управлений задача относится к числу задач классического вариационного исчисления. Но
формальной попытке составить уравнения Эйлера-Лагранжа препятствует то, что мощность, а
отсюда и гамильтониан не дифференцируемы в ситуации, когда или
Во-вторых, в силу отсутствия ограничений на величину
управлений задача относится к числу задач классического вариационного исчисления. Но
формальной попытке составить уравнения Эйлера-Лагранжа препятствует то, что мощность, а
отсюда и гамильтониан не дифференцируемы в ситуации, когда или ![]() , или
, или ![]() .
Показано, что экстремали находятся среди управляемых траекторий, для которых
.
Показано, что экстремали находятся среди управляемых траекторий, для которых ![]() , если
, если
![]() ,
, ![]() , если
, если
![]() и
и ![]() , если
, если
![]() . Здесь
. Здесь
![]() .
.
Теорема 4.1. На оптимальном перемещении цилиндра мощность не изменяет своего
значения. Производная мощности по скорости точки захвата вне интервалов движения, во
время которых
![]() , также сохраняет постоянное значение.
, также сохраняет постоянное значение.
Затем установлено, что существуют экстремали только трех типов. Первая из них
соответствует движению цилиндра с сохранением вертикальной ориентации и с постоянной
скоростью точки захвата. Уравнения движения в соответствии со второй экстремалью в
промежутке времени ![]() приведены к виду, удобному для организации вычислительного
процесса для нахождения текущих оптимальных значений скоростей
приведены к виду, удобному для организации вычислительного
процесса для нахождения текущих оптимальных значений скоростей ![]() и
и ![]() , а именно:
, а именно:
Условия сопряжения экстремальных дуг дают возможность выписать выражения для двух углов
![]() и
и ![]() , позволяющие определить угол, начиная с которого цилиндр
должен двигаться с ориентацией, обеспечивающей равенство
, позволяющие определить угол, начиная с которого цилиндр
должен двигаться с ориентацией, обеспечивающей равенство ![]() . Такой режим назван
скольжением, так как в ходе него цилиндр движется с нулевым углом атаки. Скольжение
описывается системой (5.6) при условии, что мощность постоянна и
. Такой режим назван
скольжением, так как в ходе него цилиндр движется с нулевым углом атаки. Скольжение
описывается системой (5.6) при условии, что мощность постоянна и ![]() . Такая
система интегрируется до конца, при этом
. Такая
система интегрируется до конца, при этом
Если относительное удлинение цилиндра ![]() , то можно выбрать интервал чисел
Рейнольдса
, то можно выбрать интервал чисел
Рейнольдса
![]() , на котором известны данные по значениям
коэффициентов лобового сопротивления цилиндров с образующими как перпендикулярными, так и
параллельными потоку (см., например, [12]. Практически, эти значения не зависят от
числа Рейнольдса. Эта информация положена в основу интерполирования коэффициентов
лобового сопротивления цилиндра по двум переменным - относительному удлинению и углу
атаки. Оптимальные скорости
, на котором известны данные по значениям
коэффициентов лобового сопротивления цилиндров с образующими как перпендикулярными, так и
параллельными потоку (см., например, [12]. Практически, эти значения не зависят от
числа Рейнольдса. Эта информация положена в основу интерполирования коэффициентов
лобового сопротивления цилиндра по двум переменным - относительному удлинению и углу
атаки. Оптимальные скорости ![]() и
и ![]() ищутся среди тех, которые обеспечивают
удержание чисел Рейнольдса на указанном выше интервале. Тогда интерполированные
коэффициенты лобового сопротивления - медленно изменяющиеся функции числа Рейнольдса и,
следовательно, выполняется гипотеза 2 раздела 1.
ищутся среди тех, которые обеспечивают
удержание чисел Рейнольдса на указанном выше интервале. Тогда интерполированные
коэффициенты лобового сопротивления - медленно изменяющиеся функции числа Рейнольдса и,
следовательно, выполняется гипотеза 2 раздела 1.
Предварительный теоретический анализ позволяет установить интервалы знакопостоянства
параметров ![]() ,
, ![]() и
и ![]() . Оказывается, что
. Оказывается, что ![]() ,
, ![]() для
для
![]() и
и ![]() для
для
![]() , где
, где
![]() . Кроме этого, установлено существование
двух универсальных констант
. Кроме этого, установлено существование
двух универсальных констант ![]() и
и ![]() , которые позволили классифицировать
и описать структуру второй экстремали. Если
, которые позволили классифицировать
и описать структуру второй экстремали. Если
![]() , то сход в режим
скольжения происходит по достижению угла
, то сход в режим
скольжения происходит по достижению угла
![]() . В противном случае это происходит на углу
. В противном случае это происходит на углу ![]() . Если
. Если
![]() , то угол
, то угол
![]() , в противном случае угол
, в противном случае угол
![]() . Полученная информация о структуре системы
(5.8)-(5.13), являясь полезной, не снимает трудность ее численного
интегрирования. Дело в том, что хотя система(5.8)-(5.13) выписана в
нормальной форме Коши, она определяет
. Полученная информация о структуре системы
(5.8)-(5.13), являясь полезной, не снимает трудность ее численного
интегрирования. Дело в том, что хотя система(5.8)-(5.13) выписана в
нормальной форме Коши, она определяет ![]() ,
, ![]() лишь неявным образом. Это
затруднение преодолевается введением для угла
лишь неявным образом. Это
затруднение преодолевается введением для угла ![]() запаздывания по времени, и
вычислительный процесс осуществляется по следующей схеме. Пусть в момент
запаздывания по времени, и
вычислительный процесс осуществляется по следующей схеме. Пусть в момент ![]() заданы
углы
заданы
углы ![]() и
и
![]() . Тогда можно найти угол атаки
. Тогда можно найти угол атаки
![]() , коэффициент лобового сопротивления
, коэффициент лобового сопротивления
![]() , коэффициент
, коэффициент ![]() , корень уравнения (5.12). Затем по формулам
(5.10), (5.11) можно подсчитать угол
, корень уравнения (5.12). Затем по формулам
(5.10), (5.11) можно подсчитать угол ![]() , а по формуле
(5.9) - скорость перемещения центра масс
, а по формуле
(5.9) - скорость перемещения центра масс ![]() . Эта информация позволит
определить правые части системы (5.8) в момент
. Эта информация позволит
определить правые части системы (5.8) в момент ![]() . После этого обобщенные
координаты цилиндра
. После этого обобщенные
координаты цилиндра ![]() ,
,
![]() в следующий момент
в следующий момент ![]() находятся, например, по формуле метода Рунге - Кутта. На рис. 2 представлены
графики изменения обобщенных скоростей, угла атаки и скорости центра инерции цилиндра в
функции его угловой координаты.
находятся, например, по формуле метода Рунге - Кутта. На рис. 2 представлены
графики изменения обобщенных скоростей, угла атаки и скорости центра инерции цилиндра в
функции его угловой координаты.
![\includegraphics[%height=0.4\textheight,
width=0.7\textwidth]{c:/marinov/tom6rus/final2/zaval/cylgr42.eps}](img286.gif)
При интегрировании системы (5.8)-(5.13) необходимо на каждом шаге решать уравнение (5.12). Главная особенность этого уравнения состоит в неединственности его решений. Разработан алгоритм, который обеспечивает удержание нужного корня на нужной ветви решений уравнения (5.12) и в случае исчезновения этой ветви переводит его на другую ветвь. Чтобы найти нужный корень на очередном шаге интегрирования системы (без ``срыва'' на чужую ветвь), применяется специальная процедура. Она состоит в нахождении для искомого корня симметричного интервала. Эти и другие алгоритмические особенности, сопровождающие решение рассматриваемой задачи, детально обсуждаются в [28].
Вычислительный эксперимент позволил сделать вывод, что на всех удлинениях ![]() из
интервала (0.4, 4.2) вторая экстремаль не может дать результат лучше, чем третья. Система
(5.6) интегрируется в квадратурах как в случае движения цилиндра в соответствии с
первой экстремалью, так и с третьей. Это дает возможность сравнения первой и третьей
экстремалей уже аналитическими методами.
из
интервала (0.4, 4.2) вторая экстремаль не может дать результат лучше, чем третья. Система
(5.6) интегрируется в квадратурах как в случае движения цилиндра в соответствии с
первой экстремалью, так и с третьей. Это дает возможность сравнения первой и третьей
экстремалей уже аналитическими методами.
В результате установлены следующие факты. Если относительное удлинение цилиндра превышает
величину ![]() и отношение
и отношение ![]() больше, чем некоторое критическое значение
больше, чем некоторое критическое значение
![]() , зависящее от
, зависящее от ![]() , тогда третья экстремаль является оптимальной. В
противном случае оптимальным является движение цилиндра с сохранением вертикальной
ориентации и с постоянной скоростью. Здесь
, тогда третья экстремаль является оптимальной. В
противном случае оптимальным является движение цилиндра с сохранением вертикальной
ориентации и с постоянной скоростью. Здесь ![]() и
и
![]() - корни
некоторых трансцендентных уравнений. Значение
- корни
некоторых трансцендентных уравнений. Значение ![]() как функция относительного
удлинения цилиндра неограниченно и монотонно возрастает при
как функция относительного
удлинения цилиндра неограниченно и монотонно возрастает при
![]() .
.
Исходную задачу можно решить как обратную задачу динамики. Действительно, информация об
оптимальных управлениях в задаче 4.2 является по сути дела информацией об оптимальных
фазовых траекториях в исходной задаче 4.1. Следовательно, достаточно подставить
оптимальные ![]() и
и ![]() в уравнения движения цилиндра:
в уравнения движения цилиндра:
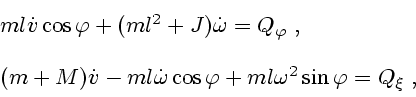
![\begin{displaymath}
\begin{array}{l}
Q_{\varphi}=-mgl\sin\varphi -l\bigl((D_x+D_...
...hi
)\bigl)+M_G+U\;,\\ [7pt] Q_{\xi}=D_x+D_x^l +F\;,
\end{array}\end{displaymath}](img294.gif)