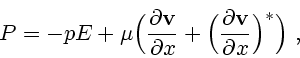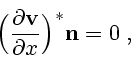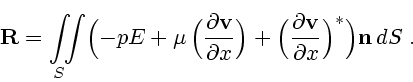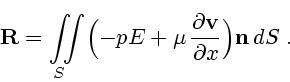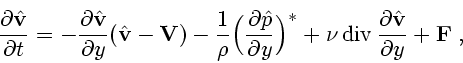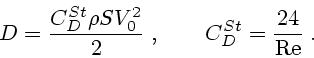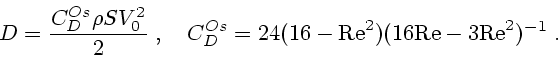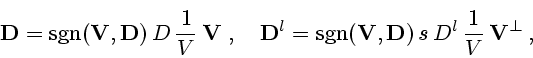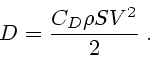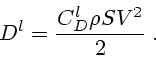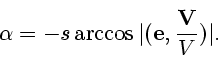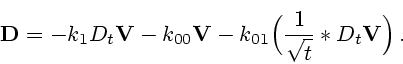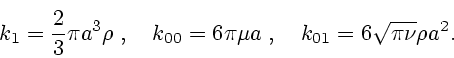

Next: 2 Оптимизация квазистационарного обтекания
Up: ZAV
Previous: Введение
В работе под термином ``среда'' понимается жидкость или газ. Однако, исходя из
интуитивных соображений, мы будем употреблять термин ``жидкость''. Ниже перечислены
гидродинамические ограничения, при выполнении которых возможно аналитическое исследование
необходимых условий оптимальности для задач, упомянутых во введении. Предполагается, что
выбрана инерциальная система, а в ней
- правая прямоугольная декартова система координат 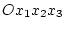 .
.
Предположим,
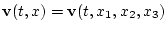 - вектор скорости частицы жидкости в
точке
- вектор скорости частицы жидкости в
точке
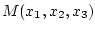 в момент
в момент 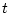 , и
, и 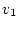 ,
, 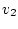 ,
, 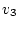 - компоненты
- компоненты 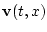 . Первые два ограничения сводятся к следующему.
. Первые два ограничения сводятся к следующему.
L1. Жидкость несжимаема.
С учетом уравнения неразрывности это ограничение эквивалентно тому, что скорость объемной
деформации равна нулю:
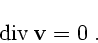 |
(1.1) |
L2. Выполняется обобщенная гипотеза Ньютона [22]
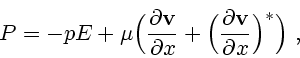 |
(1.2) |
где 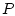 - линейный оператор, определяемый тензором напряжений,
- линейный оператор, определяемый тензором напряжений, 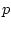 - скалярное поле
давления,
- скалярное поле
давления, 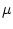 - коэффициент динамической вязкости,
- коэффициент динамической вязкости, 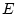 - тождественное
преобразование,
- тождественное
преобразование,
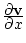 - производная Фреше,
- производная Фреше,
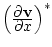 - сопряженный оператор.
- сопряженный оператор.
Пусть в жидкости движется ограниченных размеров тело с достаточно гладкой границей 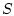 .
Одним из постулатов механики жидкости является условие прилипания: вблизи поверхности
тела векторы скорости частиц жидкости совпадают с векторами скорости соответствующих
точек поверхности тела. Из этого условия и ограничения L1 вытекает, что в случае
поступательного движения на поверхности тела выполняется равенство [22]
.
Одним из постулатов механики жидкости является условие прилипания: вблизи поверхности
тела векторы скорости частиц жидкости совпадают с векторами скорости соответствующих
точек поверхности тела. Из этого условия и ограничения L1 вытекает, что в случае
поступательного движения на поверхности тела выполняется равенство [22]
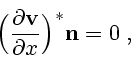 |
(1.3) |
где 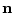 - единичный вектор внешней нормали к поверхности
- единичный вектор внешней нормали к поверхности 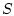 в точке
в точке 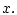
Напряжение на площадке 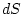 поверхности тела подсчитывается по формуле
поверхности тела подсчитывается по формуле
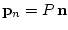 , где
, где 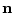 - единичный вектор внешней нормали к площадке
- единичный вектор внешней нормали к площадке 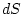 . Отсюда с учетом
(2.2) получится формула для главного вектора сил, действующих со стороны жидкости
на поверхность движущегося тела (гидродинамических сил):
. Отсюда с учетом
(2.2) получится формула для главного вектора сил, действующих со стороны жидкости
на поверхность движущегося тела (гидродинамических сил):
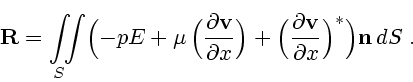 |
(1.4) |
Формула для главного момента гидродинамических сил получается аналогично. Cогласно
(2.3), если тело движется поступательно, формула (2.4) сводится к равенству
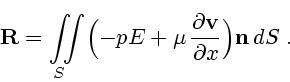 |
(1.5) |
Далее понадобится так называемая подвижная система координат
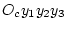 с началом в центре инерции тела и осями, жестко связанными с
телом.
с началом в центре инерции тела и осями, жестко связанными с
телом.
Для нахождения главного вектора и главного момента необходимо вычислить на поверхности
тела давление и производную Фреше вектора скорости движения жидкости. Последнее связано с
решением некоторой граничной задачи для векторного уравнения Навье-Стокса. Ниже это
уравнение выписано в подвижной системе координат
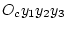 с осями, параллельными
соответствующим осям системы
с осями, параллельными
соответствующим осям системы 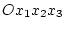 (считается, что тело движется
поступательно). Пусть
(считается, что тело движется
поступательно). Пусть 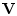 - вектор скорости движения тела и
- вектор скорости движения тела и 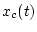 -
радиус-вектор его центра инерции. Для векторов абсолютных скоростей движения жидкости и
давления в подвижной системе координат примем обозначения
-
радиус-вектор его центра инерции. Для векторов абсолютных скоростей движения жидкости и
давления в подвижной системе координат примем обозначения
Тогда уравнение Навье-Стокса
имеет вид
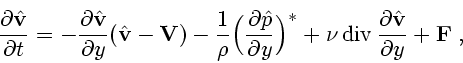 |
(1.6) |
где 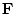 - напряженность поля силы тяжести,
- напряженность поля силы тяжести, 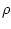 - плотность жидкости,
- плотность жидкости,
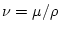 - коэффициент кинематической вязкости.
- коэффициент кинематической вязкости.
Теперь упомянутая выше граничная задача сводится к нахождению решения системы уравнений в
частных производных, состоящей из уравнения (2.6) и уравнения неразрывности
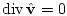 . Это решение должно удовлетворять условию прилипания
. Это решение должно удовлетворять условию прилипания
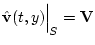 , а также естественному условию вида
, а также естественному условию вида
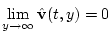 .
.
Обтекание называется установившимся, если поле его абсолютных скоростей в подвижной
системе не изменяется с течением времени. Ясно, что в случае поступательного движения
тела стационарное обтекание возможно лишь при условии, что
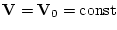 .
.
Ниже приведены формулы для силы лобового сопротивления, действующей на однородный шар, в
стационарных случаях, рассмотренных Стоксом и Озееном.
Метод Стокса пренебрегает в уравнении (2.6) напряженностью гравитационного поля и
слагаемым
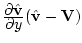 . В
результате для величины силы сопротивления движению шара получается выражение
. В
результате для величины силы сопротивления движению шара получается выражение
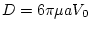 , где
, где 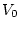 есть величина вектора скорости
есть величина вектора скорости 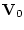 ,
, 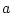 - радиус шара. Для
последующих обобщений этому выражению удобно придать форму
- радиус шара. Для
последующих обобщений этому выражению удобно придать форму
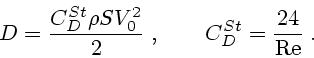 |
(1.7) |
Здесь 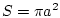 ,
, 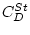 - коэффициент лобового сопротивления,
- коэффициент лобового сопротивления,
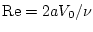 - число Рейнольдса.
- число Рейнольдса.
Подход Озеена по-прежнему пренебрегает действием гравитационных сил и квадратичными
членами инерции, но полностью учитывает скорость движения шара в уравнении Навье-Стокса.
Получается следующий приближенный результат:
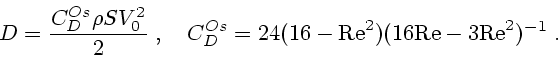 |
(1.8) |
Пусть тело обладает осью симметрии. Тогда в случае движения, в процессе которого его ось
симметрии не покидает заданной плоскости, например, вертикальной плоскости 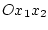 ,
согласно теоремам статики абсолютно твердого тела система сил воздействия жидкости на
тело может быть приведена к равнодействующей, называемой гидродинамической силой. Как
принято (см., например, [23]), точка пересечения оси симметрии с линией действия
гидродинамической силы называется центром давления. Эту силу обычно разлагают на две
составляющие, первая из которых имеет направление, коллинеарное вектору скорости движения
центра инерции тела
,
согласно теоремам статики абсолютно твердого тела система сил воздействия жидкости на
тело может быть приведена к равнодействующей, называемой гидродинамической силой. Как
принято (см., например, [23]), точка пересечения оси симметрии с линией действия
гидродинамической силы называется центром давления. Эту силу обычно разлагают на две
составляющие, первая из которых имеет направление, коллинеарное вектору скорости движения
центра инерции тела 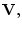 а вторая - направление, перпендикулярное
а вторая - направление, перпендикулярное 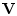 .
Первую составляющую
.
Первую составляющую 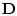 называют силой лобового сопротивления, а вторую
называют силой лобового сопротивления, а вторую 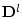 - подъемной силой.
- подъемной силой.
Пусть
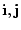 - единичные орты системы координат
- единичные орты системы координат 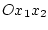 . Далее
понадобится преобразование, ставящее в соответствие вектору
. Далее
понадобится преобразование, ставящее в соответствие вектору
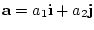 вектор
вектор
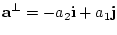 . Пусть
. Пусть 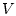 - величина вектора
скорости центра масс тела
- величина вектора
скорости центра масс тела 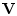 ,
, 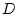 - величина силы лобового сопротивления,
- величина силы лобового сопротивления,
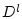 - величина подъемной силы. Справедливо утверждение, которое удобно для
последующих ссылок сформулировать в виде леммы.
- величина подъемной силы. Справедливо утверждение, которое удобно для
последующих ссылок сформулировать в виде леммы.
Лемма 1.1. Сила лобового сопротивления и подъемная сила рассчитываются по
формулам
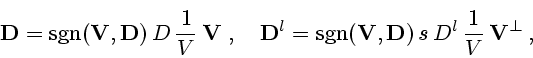 |
(1.9) |
где 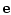 - единичный вектор, направление которого совпадает с осью симметрии
тела.
- единичный вектор, направление которого совпадает с осью симметрии
тела.
Представление (2.7) (или (2.8)) для величины действующей на шар силы лобового
сопротивления выбрано так, чтобы коэффициент 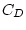 был безразмерной величиной. Это
представление можно сохранить для величины стационарной силы лобового сопротивления и в
рассматриваемом случае, т.е.
был безразмерной величиной. Это
представление можно сохранить для величины стационарной силы лобового сопротивления и в
рассматриваемом случае, т.е.
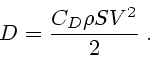 |
(1.10) |
Аналогично, величина стационарной подъемной силы представима в виде
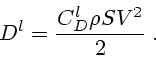 |
(1.11) |
Здесь 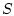 - площадь проекции тела на плоскость, перпендикулярную вектору скорости
движения его центра инерции.
- площадь проекции тела на плоскость, перпендикулярную вектору скорости
движения его центра инерции.
Согласно теории динамического подобия коэффициенты 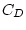 и
и 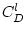 зависят только от
формы тела, чисел Рейнольдса и Фруда.
зависят только от
формы тела, чисел Рейнольдса и Фруда.
Далее рассматриваются системы из осесимметричных тел (называемых звеньями). Введем еще
одно ограничение.
L3. Движение систем происходит в объеме жидкости либо большой протяженности,
либо заключенном внутри твердых границ.
В рамках перечисленных ограничений коэффициент 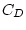 является [11] функцией только
формы тела, числа Рейнольдса и, возможно, угла атаки между вектором скорости перемещения
центра инерции тела и его осью симметрии, т.е.
является [11] функцией только
формы тела, числа Рейнольдса и, возможно, угла атаки между вектором скорости перемещения
центра инерции тела и его осью симметрии, т.е. 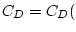 форма,
форма,
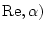 . Для
определения угла атаки можно использовать формулу
. Для
определения угла атаки можно использовать формулу
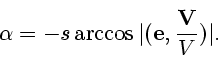 |
(1.12) |
Обращаясь к случаю нестационарного обтекания, следует отметить, что Буссинеск обобщил
подход Стокса на случай неравномерного поступательного движения шара и получил формулу
для силы лобового сопротивления [19], которая в терминах операции обобщенного
дифференцирования 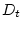 и обобщенной свертки [18] (обозначаемой ниже символом
``
и обобщенной свертки [18] (обозначаемой ниже символом
``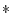 '') имеет вид
'') имеет вид
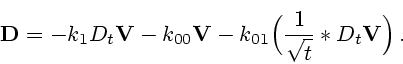 |
(1.13) |
Здесь приняты обозначения
Первый член формулы (2.13) -
инерционная составляющая сопротивления, соответствующая так называемой присоединенной
массе, а второй,
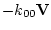 , представляет стационарную формулу Стокса.
, представляет стационарную формулу Стокса.
Если сила лобового сопротивления и подъемная сила могут быть достаточно точно описаны при
помощи формул (2.9)-(2.11), то обтекание называют
квазистационарным [11].
Далее работа гидродинамических сил рассматривается как оценка качества процесса
управления. В разделе 3 показано, что решение задачи об оптимальном перемещении шара в
предположении квазистационарности обтекания приводит к относительной ошибке в оптимальных
энергетических затратах всего лишь порядка 0,02 % (предполагается, что числа Рейнольдса
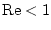 ). Нестационарность обтекания может быть частично учтена путем введения
присоединенной массы [11,12].
). Нестационарность обтекания может быть частично учтена путем введения
присоединенной массы [11,12].
Гипотеза 1. Оптимальное перемещение системы порождает квазистационарное
обтекание ее звеньев.
Лемма 1.2. Пусть выполнены ограничения L1-L3, справедлива гипотеза 1 и коэффициент лобового сопротивления каждого звена системы является однородной
функцией степени 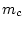 чисел Рейнольдса, соответствующих оптимальному движению системы.
Тогда для каждого звена величина силы лобового сопротивления является однородной функцией
степени
чисел Рейнольдса, соответствующих оптимальному движению системы.
Тогда для каждого звена величина силы лобового сопротивления является однородной функцией
степени 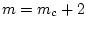 от величины скорости его центра инерции. То же самое верно и для
подъемных сил.
от величины скорости его центра инерции. То же самое верно и для
подъемных сил.
Замечание. Для тел сферической или цилиндрической формы коэффициент
лобового сопротивления является практически однородной функцией достаточно малых чисел
Рейнольдса, когда он приблизительно обратно пропорционален им, а также достаточно больших
чисел Рейнольдса, когда он незначительно зависит от них (в частности, такие числа
образуют довольно протяженную левую полуокрестность числа
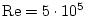 ). В
первом случае
). В
первом случае 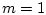 , а во втором
, а во втором 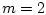 .
.
Гипотеза 2. Оптимальные перемещения систем обладают следующим свойством: числа
Рейнольдса, соответствующие каждому звену, таковы, что коэффициенты лобового
сопротивления и подъемной силы звена являются однородными функциями некоторой степени
этих чисел.


Next: 2 Оптимизация квазистационарного обтекания
Up: ZAV
Previous: Введение
2003-06-25