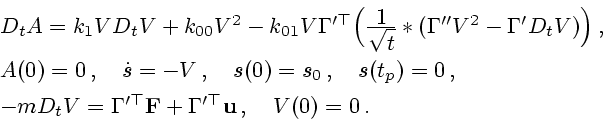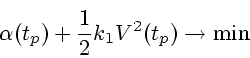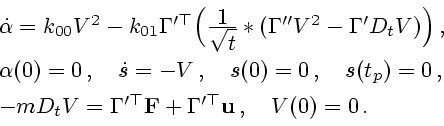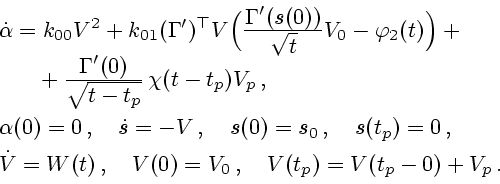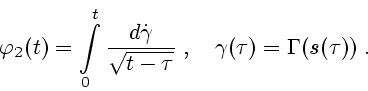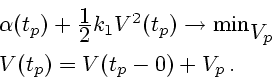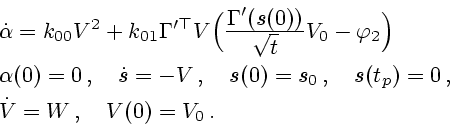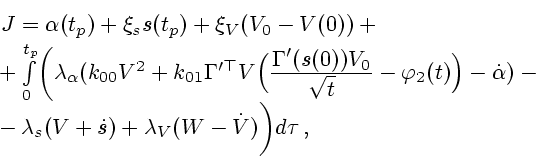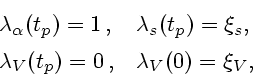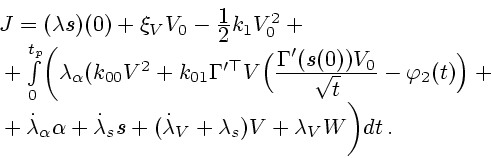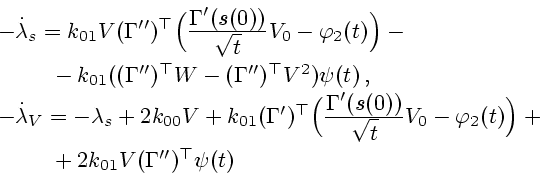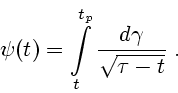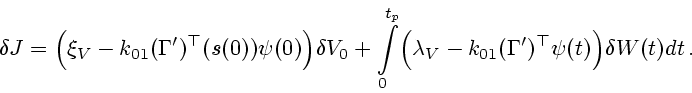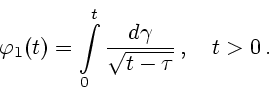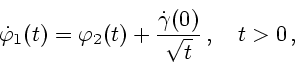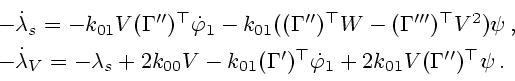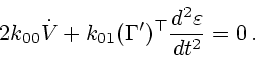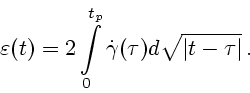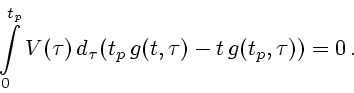

Next: 4 Движение цилиндра в
Up: ZAV
Previous: 2 Оптимизация квазистационарного обтекания
Снова исследуется задача, поставленная
в разделе 2. При этом предполагается, что выполнены ограничения L1-L2 и движение шара происходит в
неограниченном объеме жидкости (т.е. имеет место первое из условий L3). В отличие от
раздела 2 числа Рейнольдса удовлетворяют условию 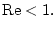 Для расчета силы
сопротивления жидкости используется формула Буссинеска (2.13).
Для расчета силы
сопротивления жидкости используется формула Буссинеска (2.13).
Выражение для мощности силы лобового сопротивления имеет вид
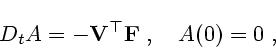 |
(3.1) |
Задача 3.1. Требуется найти вектор-функцию 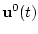 ,
,
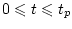 ,
минимизирующую функционал
,
минимизирующую функционал 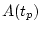 при динамических связях
при динамических связях 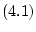 и
и 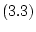 ,
ограничении на фазовые координаты шара
,
ограничении на фазовые координаты шара 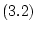 и граничном условии
и граничном условии
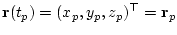 .
.
Поставленная задача имеет следующие особенности. Динамическая
связь (3.3)
есть сверточное уравнение в обобщенных функциях. Действительно, подставляя выражение
(2.13) в (3.4), после несложных преобразований можно получить соотношение
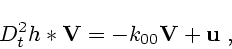 |
(3.2) |
где
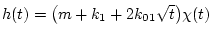 ,
, 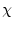 - функция Хевисайда
единичного скачка. Очевидно, порядок сингулярности [18] распределения
- функция Хевисайда
единичного скачка. Очевидно, порядок сингулярности [18] распределения 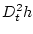 равен 2. Задача не предполагает каких-либо геометрических ограничений на управляющую
силу. Как показывает опыт [13,17] в такой ситуации в составе оптимальной
управляющей силы могут появиться импульсные составляющие. Тогда при вычислении работы
силы сопротивления жидкости возникает необходимость умножить разрывную скорость шара на
ее обобщенную производную, что связано с так называемой проблемой умножения обобщенных
функций. Поэтому попытка решить задачу 3.1 при помощи известных классических вариационных
процедур некорректна.
равен 2. Задача не предполагает каких-либо геометрических ограничений на управляющую
силу. Как показывает опыт [13,17] в такой ситуации в составе оптимальной
управляющей силы могут появиться импульсные составляющие. Тогда при вычислении работы
силы сопротивления жидкости возникает необходимость умножить разрывную скорость шара на
ее обобщенную производную, что связано с так называемой проблемой умножения обобщенных
функций. Поэтому попытка решить задачу 3.1 при помощи известных классических вариационных
процедур некорректна.
Задача 3.1 относится к числу задач динамической оптимизации с ограничениями в виде
равенств на фазовые переменные. В данном случае есть возможность перейти к задаче без
таких ограничений. Именно, последовательное дифференцирование по времени (3.2)
приводит к формулам
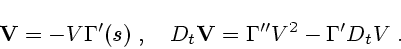 |
(3.3) |
Эти формулы и равенства
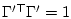 ,
,
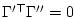 позволяют перейти от исходной задачи 3.1 к эквивалентной задаче
позволяют перейти от исходной задачи 3.1 к эквивалентной задаче
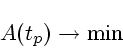 |
(3.4) |
В задаче 3.1 и, следовательно, в задаче (4.4) выражение для мощности содержит
произведение 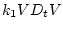 . Если в момент
. Если в момент 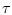 скорость шара претерпевает скачoк, то этот
скачок необходимо далее умножить на импульсную функцию Дирака, с носителем в том же
моменте времени. Ниже используется корректное определение такого произведения
скорость шара претерпевает скачoк, то этот
скачок необходимо далее умножить на импульсную функцию Дирака, с носителем в том же
моменте времени. Ниже используется корректное определение такого произведения
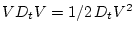 [13]. Это определение дает возможность представить работу в
виде
[13]. Это определение дает возможность представить работу в
виде
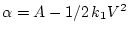 и преобразовать задачу (4.4) к следующей:
и преобразовать задачу (4.4) к следующей:
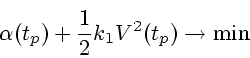 |
(3.5) |
Итак, исходная задача 3.1 преобразована к задаче (4.5).
Последняя не содержит
ограничений на фазовые координаты шара и произведений обобщенных функций.
Последний шаг редукции связан с введением нового управления 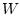 , описывающего
составляющую ускорения шара вдоль кривой
, описывающего
составляющую ускорения шара вдоль кривой 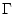 , т.е.
, т.е. 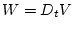 . Согласно
(4.2), (4.3) оно связано с прежним управлением преобразованием
. Согласно
(4.2), (4.3) оно связано с прежним управлением преобразованием
Оптимальную программу 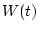 будем искать в виде
будем искать в виде
где 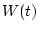 - обычная (т.е.
интегрируемая) функция, исчезающая вне промежутка
- обычная (т.е.
интегрируемая) функция, исчезающая вне промежутка ![$[0,t_p],$](img140.gif)
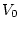 и
и 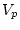 -
прозвольные константы.
-
прозвольные константы.
В результате задача (4.5), а следовательно, и исходная задача 3.1, будут сведены к
следующей.
Задача 3.2. Найти набор
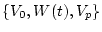 , минимизирующий функционал (4.5) при динамических связях
, минимизирующий функционал (4.5) при динамических связях
Здесь принято обозначение
Задачу 3.2 следует решать в два этапа. Сначала надо решить задачу
Очевидно, оптимальное значение
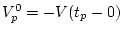 . Отсюда вытекает, что в конце
оптимального оптимального перемещения мы имеем
. Отсюда вытекает, что в конце
оптимального оптимального перемещения мы имеем
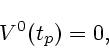 |
(3.6) |
т.е. шар должен остановиться.
Далее, поскольку величина 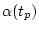 не зависит от выбора
не зависит от выбора 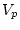 , то с учетом
(4.6) остается решить задачу
, то с учетом
(4.6) остается решить задачу
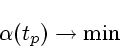 |
(3.7) |
Для этой цели можно применить классическую вариационную процедуру
Эйлера-Лагранжа [8]. Именно, пусть пара 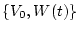 является оптимальной и
является оптимальной и
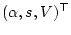 - соответствующий оптимальный процесс в задаче (4.7).
Составим функцию Лагранжа
- соответствующий оптимальный процесс в задаче (4.7).
Составим функцию Лагранжа
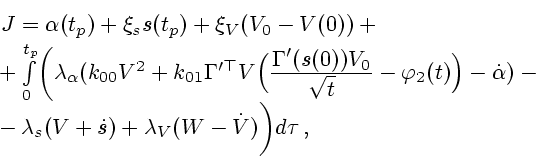 |
(3.8) |
где 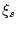 ,
, 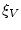 - постоянные, а
- постоянные, а
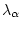 ,
, 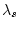 ,
, 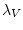 -
переменные множители Лагранжа. Проводя в (4.8) интегрирование по частям и полагая
-
переменные множители Лагранжа. Проводя в (4.8) интегрирование по частям и полагая
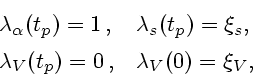 |
(3.9) |
можно привести (4.8) к виду
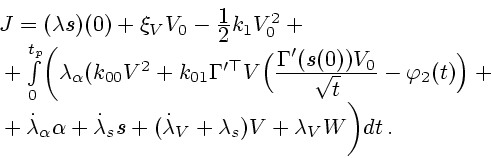 |
(3.10) |
Теперь вычислим вариацию 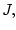 соответствующую вариациям
соответствующую вариациям 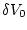 ,
, 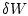 . Меняя
в полученном результате порядок интегрирования там, где это нужно, определим
. Меняя
в полученном результате порядок интегрирования там, где это нужно, определим
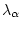 как решение уравнения
как решение уравнения
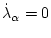 . Тогда согласно
(4.9) справедливо тождество
. Тогда согласно
(4.9) справедливо тождество
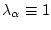 . Остальные множители
. Остальные множители 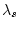 ,
, 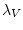 считаем решениями уравнений
считаем решениями уравнений
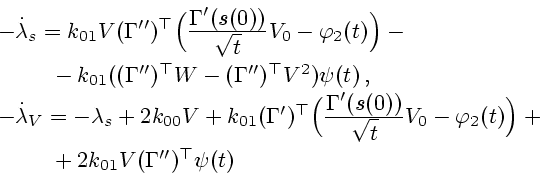 |
(3.11) |
соответственно, в которых принято обозначение
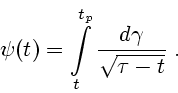 |
(3.12) |
После этого вариация 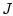 получит вид
получит вид
Эта вариация должна быть неотрицательной для любых допустимых вариаций 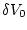 ,
,
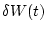 . Это с учетом последнего из соотношений (4.9), будет только тогда,
когда
. Это с учетом последнего из соотношений (4.9), будет только тогда,
когда
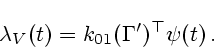 |
(3.13) |
Следует отметить, что так определенный множитель Лагранжа удовлетворяет третьему и
четвертому из равенств (4.9).
Определим вектор-функцию
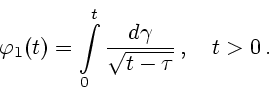 |
(3.14) |
Справедливо тождество
при помощи которого сопряженная система
(4.11) может быть записана в виде
Исключая с помощью (4.13) из этих соотношений множители Лагранжа, получаем
уравнение для определения оптимальной скорости перемещения шара вдоль траектории
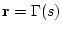 :
:
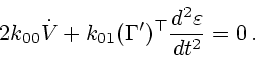 |
(3.15) |
Здесь принято обозначение
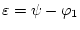 . Используя
(4.14), (4.12) можно проверить, что
. Используя
(4.14), (4.12) можно проверить, что
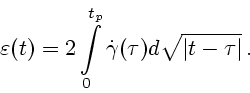 |
(3.16) |
Итак, установлено следующее утверждение.
Теорема 3.1. Оптимальная скорость перемещения шара по траектории
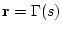 есть решение уравнений (4.15), (4.16).
есть решение уравнений (4.15), (4.16).
В случае прямолинейного движения
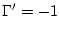 ,
,
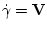 и
уравнение (4.15) допускает интеграл, который можно записать в виде интегрального
уравнения Фредгольма первого рода
и
уравнение (4.15) допускает интеграл, который можно записать в виде интегрального
уравнения Фредгольма первого рода
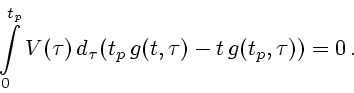 |
(3.17) |
Здесь принято обозначение
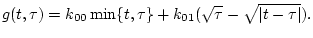
Для нахождения оптимальной скорости движения шара был разработан программно-имитационный
комплекс. При этом уравнение (4.17) приближенно решалось методом наименьших
квадратов в классе кусочно-линейных аппроксимаций с заданным числом узлов. Ниже
приводятся результаты численного эксперимента, соответствующие данным из
книги [12] по топливной нефти с плотностью 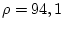 кгсек
кгсек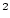 /м
/м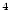 при температуре
при температуре 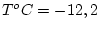 . Радиус шара
. Радиус шара 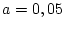 м, дальность и время пробега
м, дальность и время пробега
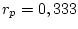 м,
м, 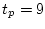 сек соответственно (в технической системе единиц МКГСС).
Анализ результатов эксперимента показывает, что значение
сек соответственно (в технической системе единиц МКГСС).
Анализ результатов эксперимента показывает, что значение 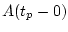 соответствует
наименьшим энергетическим в техническом смысле затратам, в то время как величина
соответствует
наименьшим энергетическим в техническом смысле затратам, в то время как величина
 - наименьшим затратам в физическом смысле на том же
перемещении. Подсчитано, что
- наименьшим затратам в физическом смысле на том же
перемещении. Подсчитано, что 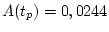 кгм. Если шар в соответствии с
оптимальной программой из раздела 2 импульсивно приводится в движение и затем
перемещается с постоянной скоростью, то энергетические затраты измеряются величиной
кгм. Если шар в соответствии с
оптимальной программой из раздела 2 импульсивно приводится в движение и затем
перемещается с постоянной скоростью, то энергетические затраты измеряются величиной
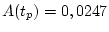 кгм, что соответствует относительной ошибке порядка
кгм, что соответствует относительной ошибке порядка 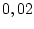 %.
Очевидно, изложенные результаты согласуются с гипотезой 1.
%.
Очевидно, изложенные результаты согласуются с гипотезой 1.


Next: 4 Движение цилиндра в
Up: ZAV
Previous: 2 Оптимизация квазистационарного обтекания
2003-06-25