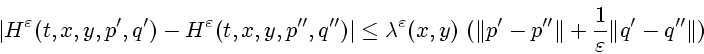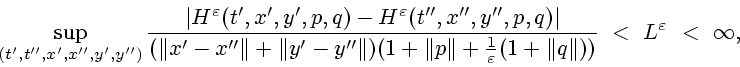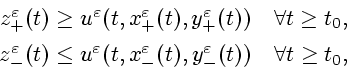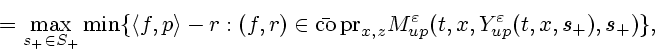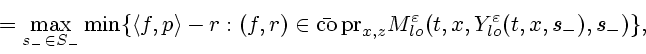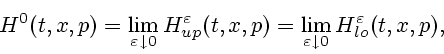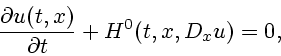2. Постановка задачи и формулировка основных результатов
Рассмотрим две задачи Коши для уравнений в
частных производных первого порядка
типа Гамильтона-Якоби: невозмущенную ![]() и сингулярно возмущенную
и сингулярно возмущенную
![]() .
.
Невозмущенная задача ![]() в фазовом пространстве
переменных
в фазовом пространстве
переменных ![]() имеет вид:
имеет вид:
Сингулярно возмущенная задача
![]() в расширенном фазовом пространстве переменных
в расширенном фазовом пространстве переменных ![]() имеет вид:
имеет вид:
где
2.1. Минимаксные решения уравнений Гамильтона-Якоби
Известно, что уравнения Гамильтона-Якоби, как правило,
не имеют глобальных классических решений [27].
Напомним определения и основные конструкции
теории минимаксных обобщенных решений
уравнений Гамильтона-Якоби [36,37,38].
Отметим прежде всего, что определение минимаксного решения УЧП первого порядка может быть сформулировано с помощью различных понятий негладкого анализа [35]: полупроизводных Дини, сопряженных производных, конусов Булигана, суб- и супердифференциалов. Определения и доказательство их эквивалентности можно найти, например, в [37,38,42].
В настоящей работе используется определение минимаксного решения, которое базируется на обобщении классического метода характеристик Коши. При таком определении классическая характеристическая система обыкновенных дифференциальных уравнений заменяется параметризованным семейством характеристических дифференциальных включений. Надграфик и подграфик минимаксного решения слабо инвариантны относительно этих дифференциальных включений. Геометрически это означает, что через любую точку надграфика (и подграфика) проходит хотя бы одна траектория дифференциального включения, которая остается в нем сколь угодно долго. Подробнее о понятии слабой инвариантности см. [1] и ссылки в этой работе.
Заметим, что характеристическими включениями в задачах Коши
![]()
![]() -
-![]() и
и
![]()
![]() -
-![]() для уравнения Айзекса являются, например, известные
в теории дифференциальных игр включения,
которые определяют свойства
для уравнения Айзекса являются, например, известные
в теории дифференциальных игр включения,
которые определяют свойства ![]() -стабильности и
-стабильности и
![]() -стабильности функции цены [23,24].
-стабильности функции цены [23,24].
Итак, напомним конструкции, с помощью которых вводится
понятие минимаксного решения в сингулярно возмущенной задаче
![]() .
.
Пусть ![]() - некоторое множество, а
- некоторое множество, а ![]() - многозначное
отображение
- многозначное
отображение
Пара
![]() называется
характеристическим комплексом (или, короче, комплексом)
в сингулярно возмущенной задаче
называется
характеристическим комплексом (или, короче, комплексом)
в сингулярно возмущенной задаче
![]()
![]() -
-![]() , если выполняются следующие условия:
, если выполняются следующие условия:
![]() для любых
для любых
![]() и
и
![]() множество
множество
![]() - непусто, выпукло и замкнуто.
Компоненты
- непусто, выпукло и замкнуто.
Компоненты
![]() удовлетворяют
неравенству
удовлетворяют
неравенству
при любых
Многозначные отображения ![]()
![]() - полунепрерывны сверху по включению
для всех
- полунепрерывны сверху по включению
для всех
![]() ;
;
![]() для любых
для любых
![]() и
и
![]() :
:
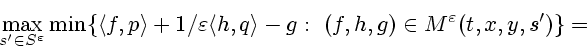
![]() для любых
для любых
![]() и
и
![]() :
:
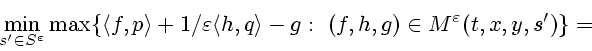
Множество всех характеристических комплексов
![]() обозначается символом
обозначается символом
![]() .
.
Пары
![]() и
и
![]() называются
верхним и нижним характеристическими комплексами
если выполняются условия
называются
верхним и нижним характеристическими комплексами
если выполняются условия ![]() и
и ![]() или соответственно условия
или соответственно условия ![]() и
и ![]() .
Множества всех верхних и нижних характеристических комплексов
.
Множества всех верхних и нижних характеристических комплексов
![]() и
и
![]() обозначаются символами
обозначаются символами
![]() и
и
![]() ,
соответственно.
,
соответственно.
Для любых
![]() и
и
![]() символом
символом
![]() обозначается
множество всех абсолютно непрерывных функций
обозначается
множество всех абсолютно непрерывных функций
![]() ,
которые удовлетворяют граничному условию
,
которые удовлетворяют граничному условию
![]() и
характеристическому дифференциальному включению
и
характеристическому дифференциальному включению
О п р е д е л е н и е 1. Полунепрерывная снизу (соответственно сверху) функция
![]() ,
называется
верхним (соответственно нижним) минимаксным решением УЧП
(2.3), если выполняется следующее условие:
,
называется
верхним (соответственно нижним) минимаксным решением УЧП
(2.3), если выполняется следующее условие:
![]() для любых
для любых
![]() (соответственно
(соответственно
![]()
![]() ),
),
![]() и
и
![]() существует траектория
существует траектория
![]() ,
такая, что
,
такая, что
![]() (соответственно
(соответственно
![]() ).
).
Здесь
![]() (соответственно
(соответственно
![]() ).
Символы
).
Символы
![]() и
и
![]() обозначают надграфик и подграфик
обозначают надграфик и подграфик ![]() соответственно, т.е.
соответственно, т.е.
З а м е ч а н и е 1. Следует подчеркнуть, что верхнее и
нижнее минимаксные решения не зависят от того , какой именно
допустимый характеристический комплекс
![]() или
или
![]() )
участвует в конструкциях определения 1.
)
участвует в конструкциях определения 1.
О п р е д е л е н и е 2. Непрерывная функция
![]() называется минимаксным решением УЧП (2.3)
тогда и только тогда, когда оно является одновременно
верхним и нижним минимаксным решением.
называется минимаксным решением УЧП (2.3)
тогда и только тогда, когда оно является одновременно
верхним и нижним минимаксным решением.
З а м е ч а н и е 2. Отметим, что характеристические дифференциальные включения
(2.8), согласованные в силу ![]() и
и ![]() с гамильтонианом
с гамильтонианом ![]() сингулярно возмущенной
задачи
сингулярно возмущенной
задачи
![]() , содержат малый
параметр
, содержат малый
параметр ![]() в качестве коэффициента перед производной переменной
в качестве коэффициента перед производной переменной
![]() , так что скорость этой переменной имеет порядок
, так что скорость этой переменной имеет порядок ![]() .
При
.
При
![]() эта скорость сколь угодно велика, поэтому
такую сингулярно возмущенную компоненту обобщенных характеристик
эта скорость сколь угодно велика, поэтому
такую сингулярно возмущенную компоненту обобщенных характеристик
![]() будем называть "быстрой переменной", а исходную
фазовую переменную
будем называть "быстрой переменной", а исходную
фазовую переменную ![]() и
и ![]() - "медленными переменными".
- "медленными переменными".
2.2. Основные предполжения и результаты
Задачи Коши ![]() и
и
![]() рассматриваются при следующих стандартных в
теории обобщенных решений УЧП первого порядка предположениях
A.1 - A.11.
рассматриваются при следующих стандартных в
теории обобщенных решений УЧП первого порядка предположениях
A.1 - A.11.
A.1 Функции
![]() - непрерывны и
ограничены, и
- непрерывны и
ограничены, и
![]() когда
когда
![]() .
.
A.2 Гамильтонианы
![]() непрерывны в области
непрерывны в области
![]() и удовлетворяют
оценкам
и удовлетворяют
оценкам
A.3 Для гамильтонианов ![]() имеют место следующие
условия Липшица относительно импульсных переменных
имеют место следующие
условия Липшица относительно импульсных переменных
A.4 Для гамильтонианов ![]() выполняются следующие
локальные условия Липшица по фазовым переменным:
выполняются следующие
локальные условия Липшица по фазовым переменным:
Доказано [37,38], что условия А.1- А.4 гарантируют
существование, единственность и эквивалентность минимаксных и
вязкостных решений
![]() в задаче
в задаче
![]() при любом
при любом
![]() . Аналогичные условия (при
. Аналогичные условия (при ![]() ) используются в
невозмущенной задаче
) используются в
невозмущенной задаче ![]() .
.
Чтобы обеспечить сходимость
минимаксных решений
![]() при
при
![]() ,
добавим следующие требования к исходным данным задачи.
,
добавим следующие требования к исходным данным задачи.
A.5 Для любого
![]() существуют верхний и
нижний характеристические комплексы
существуют верхний и
нижний характеристические комплексы
![]() и
и
![]() , у которых многозначные отображения
, у которых многозначные отображения
![]() и
и
![]() липшиц-непрерывны в метрике Хаусдорфа.
Множества параметров
липшиц-непрерывны в метрике Хаусдорфа.
Множества параметров ![]() и
и ![]() не зависят от
не зависят от ![]() , а
множества
, а
множества
![]() ,
,
![]() непрерывно зависят от
непрерывно зависят от
![]() .
.
Введем в рассмотрение следующие конструкции. Пусть
где символом
Предположим, что выполнены также следующие условия
A.6 Для любого
![]() ,
, ![]() ,
, ![]() множества
множества
![]() ,
,
![]() непусты, замкнуты и
ограничены, т.е.
непусты, замкнуты и
ограничены, т.е.
где
A.7 Для любого
![]() ,
, ![]() ,
, ![]() имеют место следующие условия Липшица
имеют место следующие условия Липшица
где
A.8 Существуют такие множества параметров
![]() и
и
![]() , что
для любого компакта
, что
для любого компакта
![]() и компактов
и компактов
![]() ,
,
![]() , стесненных требованиями
, стесненных требованиями
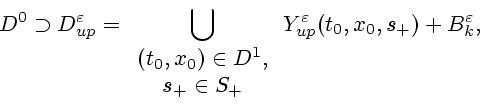
![\begin{displaymath}
D_0\supset D^\varepsilon _{lo} =
\bigcup\limits_{\begin{arra...
...-) + B^\varepsilon _{k} \
\quad \forall \varepsilon \in [0,1],
\end{displaymath}](img135.gif)
можно указать величины
![]()
![]() , когда
, когда
![]() ;
;
![]() при любых
при любых
![]() и при всех таких
и при всех таких
![]() , для которых
, для которых
где
A.9 Все константы в А.1 - A.8 и величины
![]() ,
зависящие от малого параметра
,
зависящие от малого параметра
![]() , зависят от него непрерывно.
, зависят от него непрерывно.
Введем в рассмотрение "верхний"
![]() и "нижний"
и "нижний"
![]() гамильтонианы
гамильтонианы
где символом
A.10 Пусть для любых
![]() ,
,
![]() , имеют место следующие неравенства
, имеют место следующие неравенства
Обозначим символом ![]() следующий предел
следующий предел
A.11 Предположим, что для любых
![]() ,
,
![]() ,
, ![]() справедливо
справедливо
Основной результат данной работы - достаточные условия
сходимости
![]() к
к ![]() при
при
![]() - может быть
представлен в виде следующего утверждения.
- может быть
представлен в виде следующего утверждения.
Теорема 1.
Пусть в сингулярно возмущенной задаче Коши
![]()
![]() выполняются условия
выполняются условия ![]() -
-![]() .
Тогда минимаксные решения
.
Тогда минимаксные решения
![]() этой задачи
сходятся к минимаксному решению
этой задачи
сходятся к минимаксному решению ![]() невозмущенной
задачи Коши
невозмущенной
задачи Коши
![]() (2.25) - (2.26) при
(2.25) - (2.26) при
![]() .
Эта сходимость равномерна на любых компактах
.
Эта сходимость равномерна на любых компактах
![]() ,
,
![]() .
.
Next: 3 Достаточные условия сходимости Up: SUB Previous: 1 Введение u1904 2003-06-09
![\begin{displaymath}
\sup\limits_{(t,x,y)\in [0,\th ]\times R^n\times R^k}
\frac{...
...y,0,0)\vert}{\vert(1+\Vert x\Vert+\Vert y\Vert)\vert} < \infty
\end{displaymath}](img85.gif)