3. Достаточные условия сходимости
3.1. Предварительные замечания и результаты
Условия А.1 - А.11 Теоремы 1 аналогичны предположениям теоремы о достаточных условиях сходимости из работы [41]. Новым элементом в предлагаемых выше условиях А.1 - А.11 являются соотношения (2.12), (2.13), которые определяют местонахождение аттракторов сингулярно возмущенных компонент обобщенных характеристик по их динамике.
Подобные соотношения появлялись в работе [40], где
исследовалось сингулярно возмущенное уравнение Айзекса для
дифференциальной игры с быстрыми и медленными движениями. В этой
работе в роли аттракторов выступали множества "корней" , т.е.
тех аргументов из подпространства быстрых переменных,
для которых правые части дифференциальных включений,
описывающих динамику быстрых движений, содержат нуль.
При этом свойство притяжения для множества
"корней" обеспечивалось требованием проксимального прицеливания
[11]
быстрых переменных на это множество со скоростью, пропорциональной
квадрату расстояния до множества. Такое требование обеспечивало
экспоненциальные оценки скорости сближения быстрых переменных и их
множеств притяжения, а также гарантировало сильную инвариантность
последних. Условие А.8 является обобщением предположения о
проксимальном прицеливании пропорциорально квадрату расстояния
до множества корней, которое было предложено ранее для специального
типа характеристических комплексов нелинейного уравнения
Гамильтона-Якоби (см. условия ![]() и теорему 2 в [41])
и теорему 2 в [41])
Следует сделать следующие замечания по поводу
условий А.1 - А.11.
З а м е ч а н и е 3. Предположение о существовании липшиц-непрерывных
многозначных отображений
![]() ,
определяющих характеристические комплексы из условия А.5,
не является экзотическим при выполнении стандартных
требований А.3 и А.4. Нетрудно проверить, что примером таких
комплексов могут быть пары, состоящие из множества параметров
,
определяющих характеристические комплексы из условия А.5,
не является экзотическим при выполнении стандартных
требований А.3 и А.4. Нетрудно проверить, что примером таких
комплексов могут быть пары, состоящие из множества параметров
![]() и многозначных отображений
со значениями
и многозначных отображений
со значениями
где
З а м е ч а н и е 4. Используя предположения А.5, А.9 о непрерывной зависимости от
параметра ![]() исходных данных задачи
исходных данных задачи
![]() , получаем,
что при всех
, получаем,
что при всех
![]() сходятся при
сходятся при
![]() в метрике Хаусдорфа множества
в метрике Хаусдорфа множества
Вследствие этого, а также вследствие предположения A.7,
при любых
![]() многозначные отображения
многозначные отображения
![]() являются выпукло- и компактнозначными и удовлетворяют
условию Липшица с константой
являются выпукло- и компактнозначными и удовлетворяют
условию Липшица с константой
![]() .
Из условия A.10 вытекает, что комплексы
.
Из условия A.10 вытекает, что комплексы
![]() являются соответственно верхним и нижним характеристическими
комплексами в предельной невозмущенной задаче Коши
являются соответственно верхним и нижним характеристическими
комплексами в предельной невозмущенной задаче Коши ![]()
![]() , где
гамильтониан
, где
гамильтониан ![]() имеет представление
имеет представление
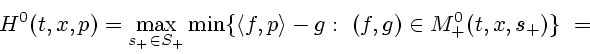
З а м е ч а н и е 5. Используя вид (3.1) и следуя определениям верхних и нижних характеристических комплексов, в условиях А.8 - А.10 можно выбрать пары:
![]()
![]()
![]()
- в качестве верхних характеристических комплексов для верхнего гамильтониана
![]()
![]()
![]()
- в качестве нижних характеристических комплексов для нижнего гамильтониана
З а м е ч а н и е 6. Для гамильтониана ![]() (2.24) в качестве верхнего и
нижнего характеристических комплексов соответственно могут
выступать пары
(2.24) в качестве верхнего и
нижнего характеристических комплексов соответственно могут
выступать пары
![]()
![]()
![]()
![]()
![]()
![]()
В этом случае хорошо известные свойства характеристических комплексов вида (3.1), замечание 5 и условия A.7 - A.10 влекут выполнение усло-
вия A.11.
Учитывая вид этих характеристических комплексов, можно
конкретизировать представление (3.2) предельного
гамильтониана ![]() следующим образом:
следующим образом:
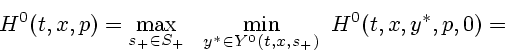
где
В дальнейшем понадобится следующий факт теории
дифференциальных включений (см. [8,14]).
Пусть
![]() -
два многозначных отображения с выпуклыми компактными
непустыми значениями, полунепрерывные сверху по включению.
Пусть
-
два многозначных отображения с выпуклыми компактными
непустыми значениями, полунепрерывные сверху по включению.
Пусть
![]() . Рассмотрим дифференциальные
включения
. Рассмотрим дифференциальные
включения
Множество решений
Утверждение 1. Для любого решения
![]() существует такое решение
существует такое решение
![]() ,
что при всех
,
что при всех
![]() справедливы оценки
справедливы оценки
3.2. Доказательство теоремы 1
Для наглядности все дальнейшие рассуждения проводятся
для верхних характеристических комплексов и соответствующих
множеств притяжения, фигурирующих в условии ![]() .
Аналогичные конструкции и утверждения для нижних
характеристических комплексов получаются с помощью
формальной замены индексов ``
.
Аналогичные конструкции и утверждения для нижних
характеристических комплексов получаются с помощью
формальной замены индексов ``![]() '' и ``+''
на ``
'' и ``+''
на ``![]() '' и ``-''.
'' и ``-''.
Пусть
![]() и, согласно A.8, для
и, согласно A.8, для ![]() множества
множества
![]() - есть множества притяжения быстрых
- есть множества притяжения быстрых
компонент
характеристических комплексов
![]() . И пусть
. И пусть
![]() , т.е.
, т.е.
Используя предположения А.5, А.7 о липшицевости в метрике
Хаусдорфа многозначных отображений
легко получим, что при всех
где, согласно условию А.8 (2.19),
а символ
Из (3.7), (3.8) следует, что динамика компонент
![]() ,
,
![]() обобщенных характеристик (3.6)
описывается с помощью дифференциальных включений
обобщенных характеристик (3.6)
описывается с помощью дифференциальных включений
Рассмотрим теперь некоторое решение
включения
Обозначим множество всех решений
Используя снова предположения А.5, А.7 о липшицевости
многозначных отображений
![]() и
и
![]() в метрике Хаусдорфа, получаем соотношения, аналогичные
(3.7),(3.8) :
в метрике Хаусдорфа, получаем соотношения, аналогичные
(3.7),(3.8) :
где
Оценим теперь расстояние между решениями
![]() дифференциального включения (3.9)
и решениями
дифференциального включения (3.9)
и решениями
![]() дифференциального включения
(3.10).
Используем для этого приведенное выше утверждение 1, где,
с учетом (3.7),(3.11),(3.12),
полагаем
дифференциального включения
(3.10).
Используем для этого приведенное выше утверждение 1, где,
с учетом (3.7),(3.11),(3.12),
полагаем
и выбираем
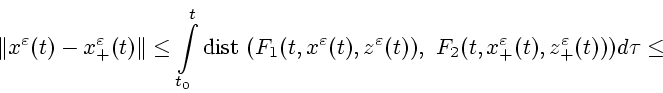
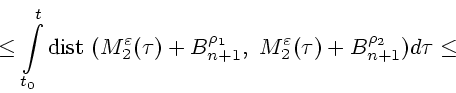
где
где
Следовательно, для разности компонент ![]() решений дифференциальных
включений (3.9) и (3.10) имеем
на отрезке
решений дифференциальных
включений (3.9) и (3.10) имеем
на отрезке
![]() оценку
оценку
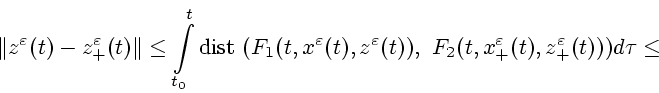
Используя предположение А.8 (2.20), получаем, что при
![]() в дифференциальном включении
(3.9), описывающем динамику
в дифференциальном включении
(3.9), описывающем динамику
![]() ,
величина
,
величина ![]() . Теперь, согласно утверждению 1, подберем
решение
. Теперь, согласно утверждению 1, подберем
решение
![]() дифференциального включения
(3.10) на отрезке
дифференциального включения
(3.10) на отрезке
![]() таким образом,
чтобы
таким образом,
чтобы
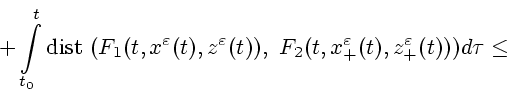
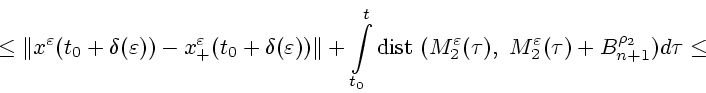
Применяя снова лемму Гронуола, получаем следующую оценку:
где
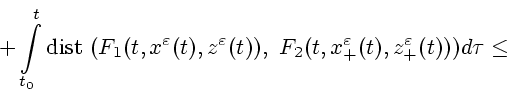
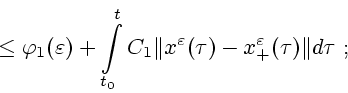
где
Суммируя вышесказанное,
и в частности замечание о том, что приведенные выше
рассуждения годятся как для верхних, так и для нижних
характеристических комплексов, фигурирующих в условии A.8,
приходим к выводу о справедливости следующего утверждения,
где величина
![]() равна
равна
![]() из предыдущих
оценок (3.17), (3.18).
из предыдущих
оценок (3.17), (3.18).
Лемма 1. Для любых компактов ![]() из условия A.8
существуют такие отображения
из условия A.8
существуют такие отображения
что
![]()
![]() при
при
![]() ;
;
![]() при любых
при любых
![]() ,
и при таких
,
и при таких
![]() , что
, что
существуют
для которых справедливы оценки
З а м е ч а н и е 7. Обозначим через
![]() область достижимости системы (3.6)
в момент времени
область достижимости системы (3.6)
в момент времени ![]() , а через
, а через
![]() -
замкнутую
-
замкнутую
![]() -окрестность
области достижимости системы (3.10).
Тогда условие (3.19) можно переписать в виде
-окрестность
области достижимости системы (3.10).
Тогда условие (3.19) можно переписать в виде
Введем в рассмотрение функции
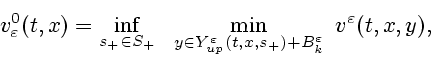
где
Конструкции типа (3.21) были введены
в работе [5] и широко используются при исследовании
вязкостных решений (см. [16]).
Лемма 2. Для любых
![]() существует точка
существует точка
![]() и точка
и точка
![]() такие, что
такие, что
Доказательство этого утверждения проводится по той же схеме, что и доказательство утверждения 1 из [39].
Полагаем теперь
Модифицируя схему доказательства утверждения 2 из [39] с учетом нестационарности множеств притяжения и условия A.8 (см. (2.18)), ослабляющего предположения из работы [41], получаем, что справедлив следующий факт.
Лемма 3. Функция
является нижним минимаксным решением задачи
Из свойств верхних и нижних минимаксных решений задачи ![]() вытекает, что при всех
вытекает, что при всех ![]()
а из условия (3.22) и построений (3.21), (3.23)-(3.24) следует
Таким образом, для всех
![]() имеем
равенство
имеем
равенство
Из оценок, полученных в лемме 1, вытекает, что сходимость в
условии (3.25) равномерна на любых выбранных компактах
![]() и
и
![]() .
.
3.3. Пример
Рассмотрим сингулярно возмущенную задачу Коши
![]() ,
где гамильтониан
,
где гамильтониан ![]() имеет вид
имеет вид
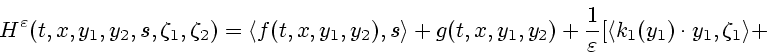
Здесь верхний и нижний характеристические комплексы могут быть выбраны следующим образом
![\begin{displaymath}
M^\varepsilon _{up}(t,x,y_1,y_2,\beta) =
\bar {\mathrm{co}}\...
...t,x,y_1,y_2), \ \frac{1}{\varepsilon }[k_1(y_1)\cdot y_1 + A],
\end{displaymath}](img339.gif)
![\begin{displaymath}
\frac{1}{\varepsilon }[k_2(y_2)\cdot y_2 + \beta], \ g(t,x,y_1,y_2) \};
\end{displaymath}](img340.gif)
![\begin{displaymath}
M^\varepsilon _{lo}(t,x,y_1,y_2,\alpha) =
\bar {\mathrm{co}}...
..._1,y_2), \ \frac{1}{\varepsilon }[k_1(y_1)\cdot y_1 + \alpha],
\end{displaymath}](img341.gif)
Соответствующие множества притяжения (аттракторы)
где
Непосредственная проверка позволяет получить экспоненциальные оценки скорости сближения быстрых компонент обобщенных характеристик
Гамильтониан ![]() в предельной невозмущенной
задаче Коши описывается формулой
в предельной невозмущенной
задаче Коши описывается формулой
![\begin{displaymath}
H^0(t,x,s) = \min\limits_{\xi_1
\in P} \max\limits_{\xi_2 \i...
...\langle f(t,x,\xi_1,\xi_2), s
\rangle + g(t,x,\xi_1,\xi_2) ] =
\end{displaymath}](img351.gif)
Верхний и нижний характеристические комплексы в невозмущенной задаче могут быть выбраны следующим образом:
Поступила 1.12.1999
Next: Bibliography Up: SUB Previous: 2 Постановка задачи и 2003-06-09
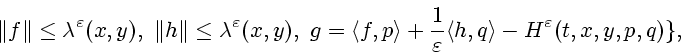
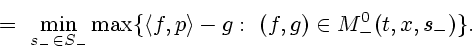
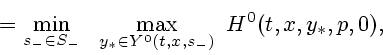
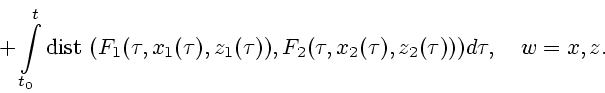
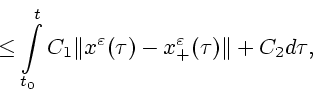
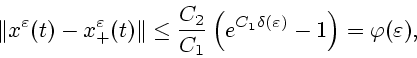
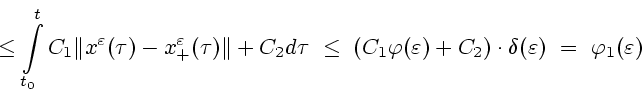
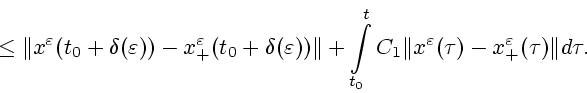
![\begin{displaymath}
\begin{array}{c}
\Vert x^\varepsilon (t) - x_\varepsilon (t)...
...при} \quad t\in [t_0 + \delta(\varepsilon ), \th ].
\end{array}\end{displaymath}](img306.gif)
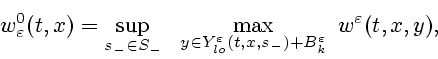
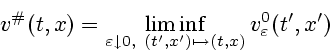
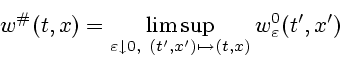
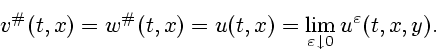
![\begin{displaymath}
+ \langle k_2(y_2) \cdot y_2, \zeta_2 \rangle
+ \min\limits_...
... +
\max\limits_{\beta \in B} \langle \zeta_2, \beta \rangle ];
\end{displaymath}](img333.gif)
![\begin{displaymath}
k_1(y_1) = \left \{
\begin{array}{l}
-1, \quad \mbox{если} \...
...\ [1ex]
-2, \quad \mbox{если} \quad y_1 < 0
\end{array}\right.
\end{displaymath}](img335.gif)
![\begin{displaymath}
k_2(y_2) = \left\{
\begin{array}{l}
-4, \quad \mbox{если} \q...
...\ [1ex]
-1, \quad \mbox{если} \quad y_2 < 0
\end{array}\right.
\end{displaymath}](img336.gif)
![\begin{displaymath}
\frac{1}{\varepsilon }[k_2(y_2) \cdot y_2 + B], \ g(t,x,y_1,y_2) \}.
\end{displaymath}](img342.gif)
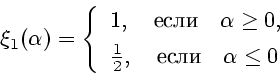
![\begin{displaymath}
\xi_2(\beta) = \left \{
\begin{array}{l}
\frac{1}{4}, \quad ...
...1ex]
1, \quad \mbox{если} \quad \beta \le 0
\end{array}\right.
\end{displaymath}](img347.gif)
![\begin{displaymath}
\max\limits_{\xi_2\in Q} \min\limits_{\xi_1 \in P}
[\langle f(t,x,\xi_1,\xi_2), s
\rangle + g(t,x,\xi_1,\xi_2) ].
\end{displaymath}](img352.gif)