Для более детального анализа процесса управления введем в рассмотрение момент
времени ![]() удовлетворяющий условиям: ранг матрицы
удовлетворяющий условиям: ранг матрицы
![]() равен
равен
![]() но ранг
но ранг
![]() Заметим, что матрица
Заметим, что матрица
![]() есть
матрица Грама, и согласно ([4, стр. 101]), rank
есть
матрица Грама, и согласно ([4, стр. 101]), rank
![]() rank
rank
![]() rank
rank
![]() При
При ![]() ядро матрицы
ядро матрицы
![]() ker
ker
![]() а все пространство
а все пространство
![]() может быть представлено в виде прямой суммы
может быть представлено в виде прямой суммы
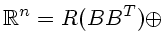 ker
ker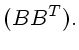
Утверждение 4.1. Для матриц
![]() ,
справедливы соотношения
,
справедливы соотношения
Д о к а з а т е л ь с т в о. В силу определения матриц
![]() (3.2) и момента
(3.2) и момента ![]() равенства
равенства
![]() ker
ker![]() ker
ker![]() очевидны при
очевидны при
![]() Далее используем метод математической
индукции.
Далее используем метод математической
индукции.
База индукции. Имеем
ker![]() ker
ker![]() так как ранг
так как ранг
![]()
Шаг индукции. Пусть при
![]() утверждение справедливо, т.е.
ker
утверждение справедливо, т.е.
ker![]() ker
ker![]() ker
ker![]() Докажем, что
ker
Докажем, что
ker![]() ker
ker![]() т.е., что если
т.е., что если
![]() ker
ker![]() то
то
![]() ker
ker![]() для всякого
для всякого ![]() -мерного вектора
-мерного вектора ![]()
Пусть
![]() ker
ker![]() тогда
тогда
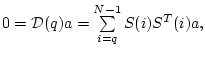 откуда следует равенство
откуда следует равенство
![]() где
где
![]() - скалярное
произведение
- скалярное
произведение![]() Распишем это равенство подробнее:
Распишем это равенство подробнее:
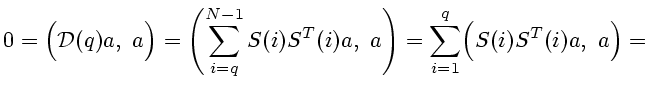
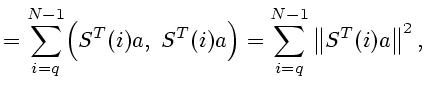
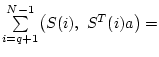
Учитывая соотношения (4.1) и (4.2), получаем
Следствие 4.1.
![]()
![]()
![]()
![]()
Таким образом, области значений матриц
![]() при
при ![]() ,
приближающемся к
,
приближающемся к ![]() , сужаются, а
ядра, соответственно, расширяются.
, сужаются, а
ядра, соответственно, расширяются.
Заметим, что похожие соотношения для образов
![]() рассмотрены в ([4, стр. 101]).
рассмотрены в ([4, стр. 101]).
Ниже будет показано, что
установленные соотношения полезны при изучении свойств оптимального управления
![]()
В заключение этого параграфа отметим следующее важное свойство псевдообратной
матрицы
![]() (см. [13, стр. 273]).
(см. [13, стр. 273]).
С в о й с т в о 4.1. На области значений
![]() матрицы
матрицы
![]() произведения
произведения
![]() и
и
![]() действуют как единичная матрица т.е. если
действуют как единичная матрица т.е. если ![]()
![]() то справедливы равенства
то справедливы равенства